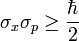So, the LHC is up and running, and has finally begun producing collisions! Seventh and Eighth-year high energy physics graduate students are celebrating (and working hard) around the world at the prospect that they might actually get their PhDs after all!
Oh, and the world hasn't been destroyed yet! For those of you who are still worried by the thought that the LHC will create a black hole and collapse the Earth in on itself, here's a web site with up-to-date information:
Has the large hadron collider destroyed the world yet?
Saturday, December 5, 2009
Thursday, November 12, 2009
Miracles
I like to think. A lot. Maybe too much.
Friends and family members always like to mention that I live in "another world". My in-laws, who speak primarily in Chinese, often like to stop mid-conversation to ask me if I understand what they're saying. My response is usually, "I wasn't listening".
Lest you think I'm being rude, it is very exhausting trying to listen to a foreign language for long periods of time. But that is not what this post is supposed to be about, so lets move on...
So, in those moments when my mind wanders, it takes me off into many directions. Sometimes they are simple thoughts like, "I wonder if I can play video games right now without my wife getting mad at me", or "How do we get the manic dog to stop barking?"
When I'm driving, I often marvel at the human brain and what it is capable of. We take for granted the complex motor skills that are required to make a simple turn. We learn the skills and practice to the point where we don't have to think any more. We think about turning and the practiced movements of our arms, feet, neck and eyes do everything for us.
I remember reading about an experiment where electrodes were placed in a monkey's brain, which transmitted signals to a robotic arm. With a little practice, the monkey could control the arm and use it almost as another limb- using the arm to grab treats and feed itself. I wonder if this skill is related to the ability to use tools that humans and monkeys have developed as an evolutionary boost.
But that is by no means the most amazing thing I've seen.
Watching a child grow is an amazing experience. It is definitely something that might make you believe in miracles. And my daughter truly is a miracle.
When she was just a few days old, I'd watch her sleeping and see the rise and fall of her chest in time with her breathing. I'd marvel at the thought of how much had to be made just right to keep that motor running. I used to have a small fear in the back of my mind that she'd suddenly stop. That sounds morbid, but I bet every parent has had the same thought at some point or another.
After all, if you really think about it, you might realize how complex the human body is. Modern science has worked tirelessly on understanding how life works, and we have only just begun. If a baby were engineered by humans, it almost certainly wouldn't work.
But my baby can not only breathe. She can see, feel, and hear. She can learn. Every moment, she observes and learns about pieces of the world around her. She practices the skills she will eventually need in order to function as a human being- all without prodding or any incentive other than her own basic need to do so.
Through years of scientific study aimed at understanding the processes my daughter has gone through, we have learned many things. In many cases, we have learned pieces of information that we already knew in some way or another. We have learned that children need love and attention in just the same way that they need food and water. We have learned time and time again that what is best for us just happens to be what nature has provided for us all along.
In my world, miracles are everywhere. They don't have to be divinely summoned to be so.
I'd better stop before I make someone throw up.
Friends and family members always like to mention that I live in "another world". My in-laws, who speak primarily in Chinese, often like to stop mid-conversation to ask me if I understand what they're saying. My response is usually, "I wasn't listening".
Lest you think I'm being rude, it is very exhausting trying to listen to a foreign language for long periods of time. But that is not what this post is supposed to be about, so lets move on...
So, in those moments when my mind wanders, it takes me off into many directions. Sometimes they are simple thoughts like, "I wonder if I can play video games right now without my wife getting mad at me", or "How do we get the manic dog to stop barking?"
When I'm driving, I often marvel at the human brain and what it is capable of. We take for granted the complex motor skills that are required to make a simple turn. We learn the skills and practice to the point where we don't have to think any more. We think about turning and the practiced movements of our arms, feet, neck and eyes do everything for us.
I remember reading about an experiment where electrodes were placed in a monkey's brain, which transmitted signals to a robotic arm. With a little practice, the monkey could control the arm and use it almost as another limb- using the arm to grab treats and feed itself. I wonder if this skill is related to the ability to use tools that humans and monkeys have developed as an evolutionary boost.
But that is by no means the most amazing thing I've seen.
Watching a child grow is an amazing experience. It is definitely something that might make you believe in miracles. And my daughter truly is a miracle.
When she was just a few days old, I'd watch her sleeping and see the rise and fall of her chest in time with her breathing. I'd marvel at the thought of how much had to be made just right to keep that motor running. I used to have a small fear in the back of my mind that she'd suddenly stop. That sounds morbid, but I bet every parent has had the same thought at some point or another.
After all, if you really think about it, you might realize how complex the human body is. Modern science has worked tirelessly on understanding how life works, and we have only just begun. If a baby were engineered by humans, it almost certainly wouldn't work.
But my baby can not only breathe. She can see, feel, and hear. She can learn. Every moment, she observes and learns about pieces of the world around her. She practices the skills she will eventually need in order to function as a human being- all without prodding or any incentive other than her own basic need to do so.
Through years of scientific study aimed at understanding the processes my daughter has gone through, we have learned many things. In many cases, we have learned pieces of information that we already knew in some way or another. We have learned that children need love and attention in just the same way that they need food and water. We have learned time and time again that what is best for us just happens to be what nature has provided for us all along.
In my world, miracles are everywhere. They don't have to be divinely summoned to be so.
I'd better stop before I make someone throw up.
Sunday, November 1, 2009
Physicists are Everywhere
For those of you who don't really know what goes on in the world of experimental physics, let me tell you about what I've been doing the last couple weeks.
So, I've posted about the KATRIN project before, but here's a recap: KATRIN is a project that aims to directly measure the neutrino mass by examining the beta-decay spectrum of tritium. The specific part I'm working on is the rear section, which is an important calibration piece of the experiment. For the output of the experiment to make sense, we need to know precisely how much tritium there is in the system at any given time. To accomplish this, we use a detector in the back wall to count the electrons that don't make it through the main spectrometer.
Now, I've been examining one potential problem with this picture- one having to do with electron scattering. You see, the beta decay electrons don't just travel around until they hit the detector- they can also scatter by interacting with the tritium in the column. These interactions make the electrons lose energy, and happen with more frequency when the tritium density increases. With less energy, the electrons are then less likely to be counted in the back end, and this introduces a systematic uncertainty into the measurement of the tritium density.
So, to explore the problem, I wrote a monte carlo program that shows the effect that electron scattering actually has. My program first randomly selects where the electron is emitted from, and at which angle. Then the program selects how far it gets before it scatters, and how much energy it loses. If the electron hasn't reached the wall, the process repeats until it does. Then, the program repeats the whole process again until it has simulated 100,000 electrons. Then, I ran my output through my professor's code, which does a similar thing with the detector design we're using. Altogether, these simulations show what we should expect as an output, should we see some variation in the tritium density, and gives a baseline for the systematic uncertainties we should expect. It also gives us some commentary on the feasibility of the detector design.
I have a point, but you'll have to read on.
At the beginning of baseball season every year, you can usually find some article online talking about computer algorithms that predict the outcomes of the coming season. These algorithms calculate how many games a team will win, how many runs they will score, their likelihood of making the playoffs, and much more. The way they do it is actually quite simple (in principle).
These algorithms merely take the rosters of each team, and uses each players' projected stats to calculate the likelihood of every possible outcome of any particular pitcher-batter match-up. Using these stats, the algorithms simulate every game of the season, one plate appearance at a time. They then repeat the algorithm about a thousand times to minimize uncertainties in random variations.
Hopefully you're starting to see a pattern. Here's another example:
Last fall, I watched a few episodes of a show called "Deadliest Warrior". The premise of the show is that they explore and analyze the weapons and fighting techniques of some of history's most famous warriors, and try to answer the question of who was more lethal. It's the perfect show for any guy who has ever sat around drinking with his buddies and asked the question, "Hey, if a samurai and a viking ever fought to the death, who would win?" The answer, of course- the samurai.
Anyway, so here's how the show went about answering this question: First, they invited experts and martial artists to showcase the weapons and techniques of each side, running tests on each weapon to determine its killing ability. Then, they put the data into a computer program that simulated the battle, blow by blow, a thousand times and tallied the wins for each side.
I'm not an expert in financial markets, but I'm pretty sure they do something similar there as well.
So, maybe my point is this: The work that goes on in the Physics world doesn't need to seem so distant and scary. There are many people out there who do very similar work in fields that are much more accessible to the general public.
As a matter of fact, my job is much easier than those that I highlighted earlier. My program is about 100 lines of Python code. Sports and battle simulations are much harder to do.
For example, those computer algorithms seem to predict the Yankees winning the world series every year. This year is the first since 2000 that they've been right.
...And I think we know what kind of track record the banking industry has...
So, I've posted about the KATRIN project before, but here's a recap: KATRIN is a project that aims to directly measure the neutrino mass by examining the beta-decay spectrum of tritium. The specific part I'm working on is the rear section, which is an important calibration piece of the experiment. For the output of the experiment to make sense, we need to know precisely how much tritium there is in the system at any given time. To accomplish this, we use a detector in the back wall to count the electrons that don't make it through the main spectrometer.
Now, I've been examining one potential problem with this picture- one having to do with electron scattering. You see, the beta decay electrons don't just travel around until they hit the detector- they can also scatter by interacting with the tritium in the column. These interactions make the electrons lose energy, and happen with more frequency when the tritium density increases. With less energy, the electrons are then less likely to be counted in the back end, and this introduces a systematic uncertainty into the measurement of the tritium density.
So, to explore the problem, I wrote a monte carlo program that shows the effect that electron scattering actually has. My program first randomly selects where the electron is emitted from, and at which angle. Then the program selects how far it gets before it scatters, and how much energy it loses. If the electron hasn't reached the wall, the process repeats until it does. Then, the program repeats the whole process again until it has simulated 100,000 electrons. Then, I ran my output through my professor's code, which does a similar thing with the detector design we're using. Altogether, these simulations show what we should expect as an output, should we see some variation in the tritium density, and gives a baseline for the systematic uncertainties we should expect. It also gives us some commentary on the feasibility of the detector design.
I have a point, but you'll have to read on.
At the beginning of baseball season every year, you can usually find some article online talking about computer algorithms that predict the outcomes of the coming season. These algorithms calculate how many games a team will win, how many runs they will score, their likelihood of making the playoffs, and much more. The way they do it is actually quite simple (in principle).
These algorithms merely take the rosters of each team, and uses each players' projected stats to calculate the likelihood of every possible outcome of any particular pitcher-batter match-up. Using these stats, the algorithms simulate every game of the season, one plate appearance at a time. They then repeat the algorithm about a thousand times to minimize uncertainties in random variations.
Hopefully you're starting to see a pattern. Here's another example:
Last fall, I watched a few episodes of a show called "Deadliest Warrior". The premise of the show is that they explore and analyze the weapons and fighting techniques of some of history's most famous warriors, and try to answer the question of who was more lethal. It's the perfect show for any guy who has ever sat around drinking with his buddies and asked the question, "Hey, if a samurai and a viking ever fought to the death, who would win?" The answer, of course- the samurai.
Anyway, so here's how the show went about answering this question: First, they invited experts and martial artists to showcase the weapons and techniques of each side, running tests on each weapon to determine its killing ability. Then, they put the data into a computer program that simulated the battle, blow by blow, a thousand times and tallied the wins for each side.
I'm not an expert in financial markets, but I'm pretty sure they do something similar there as well.
So, maybe my point is this: The work that goes on in the Physics world doesn't need to seem so distant and scary. There are many people out there who do very similar work in fields that are much more accessible to the general public.
As a matter of fact, my job is much easier than those that I highlighted earlier. My program is about 100 lines of Python code. Sports and battle simulations are much harder to do.
For example, those computer algorithms seem to predict the Yankees winning the world series every year. This year is the first since 2000 that they've been right.
...And I think we know what kind of track record the banking industry has...
Tuesday, September 29, 2009
Irrational Emotion
So, football season has been going for a couple weeks now, and as my wife can attest to, I think I've been a little too preoccupied over the weekends. I've been a little puzzled myself as to why.
Football never struck me as all that great a sport. I always thought there were too many players, too many positions, and definitely too many rules. I never liked how one player, the quarterback, can account for seemingly half of a team's success (and take all the credit). I especially despised those stupid touchdown celebrations. In baseball, acting like that after a hitting a home run would probably result in getting beamed in the hip by a fastball in your next at-bat.
But then I went to college and found out a fact that I hadn't even considered before- I suddenly had a team to root for. I followed my team's highs and lows (in that order) year after year until my head was about to explode.
Now I'm a little better versed in football terminology and have developed an appreciation for the game. After doing a quick search on wikipedia, I can tell you a little about the different positions. I can tell you the difference between the 4-3 and 3-4. I also notice a few basic things when I watch- like how bad things happen when you don't get to the quarterback and why good time management is so important.
That being said, I'm still a bit confused over a few things: What's the difference between a running back and a tail back? How do you tell a chop block from a crackback? Why are wide receivers the only ones with the attitude problems?
And I still get confused by lines like "great lead-blocking in the backfield." I also get fooled by play-action way too often. It's a good thing I'm not a linebacker because I have a habit of losing sight of the football.
And now, after a particularly gruesome loss by my once-promising team (for about the fifth year in a row), I'm pondering why I've once again decided to devote so much energy to this futile endeavor.
To answer that question, I'll refer to an experiment I recently learned about from the field of group psychology. In this experiment, participants were paired up and played several sequences of the prisoner's dilemma game through a computer interface (so they couldn't see each other). (If you're not familiar with the prisoner's dilemma, it is enough to know that each person is given the option of either cooperating or backstabbing the other participant).
What made this experiment interesting was that the participants were told one bit of information about their partners prior to playing. This bit of information could be one of several things, including race, gender, taste in music, favorite ice cream flavor, or just about anything else.
The experimenters found that people were much more likely to cooperate with their partners when the bit of information they were told showed similarities with themselves. In other words, they treated people better when they were of the same race, gender, or even liked the same ice cream.
Even more astonishing was the result of the next experiment. In this next experiment, participants played the prisoner's dilemma game once again, but this time, they were placed in random groups. The participants never met each other face-to-face, were aware that the groups were selected randomly, and never learned any information about their partners apart from which group they belonged to.
Despite the fact that these groups were formed randomly, the participants showed the same favoritism for those in the same group that they showed for those with the same race in the first experiment. In many cases they weren't even aware that they showed this favoritism.
What do we learn from this experiment? I think it has powerful implications concerning the nature of human existence. We underestimate the importance of our group memberships in our everyday lives. This experiment shows that we cannot help but identify ourselves as members of certain groups, regardless of whether or not the organization of those groups shows any sense of logic or reason. It is an interesting (and somewhat frightening) prospect.
So in the context of this experiment, I suppose it becomes perfectly natural to root for a team that represents your school or the area where you grew up. If you really think about it, those players really have very little in common with us fans (I've never seen a burly offensive lineman squeeze into a chair at one of my physics lectures), but I suppose I'm just looking for a reason to root for someone. Any reason will do.
That seems fine to me.
Football never struck me as all that great a sport. I always thought there were too many players, too many positions, and definitely too many rules. I never liked how one player, the quarterback, can account for seemingly half of a team's success (and take all the credit). I especially despised those stupid touchdown celebrations. In baseball, acting like that after a hitting a home run would probably result in getting beamed in the hip by a fastball in your next at-bat.
But then I went to college and found out a fact that I hadn't even considered before- I suddenly had a team to root for. I followed my team's highs and lows (in that order) year after year until my head was about to explode.
Now I'm a little better versed in football terminology and have developed an appreciation for the game. After doing a quick search on wikipedia, I can tell you a little about the different positions. I can tell you the difference between the 4-3 and 3-4. I also notice a few basic things when I watch- like how bad things happen when you don't get to the quarterback and why good time management is so important.
That being said, I'm still a bit confused over a few things: What's the difference between a running back and a tail back? How do you tell a chop block from a crackback? Why are wide receivers the only ones with the attitude problems?
And I still get confused by lines like "great lead-blocking in the backfield." I also get fooled by play-action way too often. It's a good thing I'm not a linebacker because I have a habit of losing sight of the football.
And now, after a particularly gruesome loss by my once-promising team (for about the fifth year in a row), I'm pondering why I've once again decided to devote so much energy to this futile endeavor.
To answer that question, I'll refer to an experiment I recently learned about from the field of group psychology. In this experiment, participants were paired up and played several sequences of the prisoner's dilemma game through a computer interface (so they couldn't see each other). (If you're not familiar with the prisoner's dilemma, it is enough to know that each person is given the option of either cooperating or backstabbing the other participant).
What made this experiment interesting was that the participants were told one bit of information about their partners prior to playing. This bit of information could be one of several things, including race, gender, taste in music, favorite ice cream flavor, or just about anything else.
The experimenters found that people were much more likely to cooperate with their partners when the bit of information they were told showed similarities with themselves. In other words, they treated people better when they were of the same race, gender, or even liked the same ice cream.
Even more astonishing was the result of the next experiment. In this next experiment, participants played the prisoner's dilemma game once again, but this time, they were placed in random groups. The participants never met each other face-to-face, were aware that the groups were selected randomly, and never learned any information about their partners apart from which group they belonged to.
Despite the fact that these groups were formed randomly, the participants showed the same favoritism for those in the same group that they showed for those with the same race in the first experiment. In many cases they weren't even aware that they showed this favoritism.
What do we learn from this experiment? I think it has powerful implications concerning the nature of human existence. We underestimate the importance of our group memberships in our everyday lives. This experiment shows that we cannot help but identify ourselves as members of certain groups, regardless of whether or not the organization of those groups shows any sense of logic or reason. It is an interesting (and somewhat frightening) prospect.
So in the context of this experiment, I suppose it becomes perfectly natural to root for a team that represents your school or the area where you grew up. If you really think about it, those players really have very little in common with us fans (I've never seen a burly offensive lineman squeeze into a chair at one of my physics lectures), but I suppose I'm just looking for a reason to root for someone. Any reason will do.
That seems fine to me.
Tuesday, September 8, 2009
Predictions
The following will all happen within my lifetime:
Also, I've mentioned Glenn Beck in each of the last two posts (twice in this one if you include the monkey bit). I promise to try not to in the next post.
- The word "whom" will cease to exist, as will the spelling of the word "through" (to be replaced by "thru").
- The words "they", "them" and "their" will officially be recognized as gender-neutral singular third-person pronouns (ridding us of awkward phrases like "he or she" and "his or her").
- Theoretical Physicists will finally discover the ultimate theory of everything. Knowing their work to be over, they will attempt to save their jobs by withholding the final draft and publishing false theories in order to fool governments into rewarding more grant money.
- A monkey sitting at a typewriter will write a bestseller.
- Glenn Beck and Rush Limbaugh will both be admitted into mental institutions after being diagnosed with a rare neurological disorder characterized by an inability to discern one's mouth from one's rectum.
- After a series of major advances in robotics, robots will take over the work of many occupations, including assembly line work, patient care and retail. Unemployment will skyrocket.
- After a series of major advances in artificial intelligence, robots will gain the ability to design and build other robots. Unemployment will plummet as leagues of unemployed are drafted into the military to battle the robot armies. Will Smith, Christian Bale, and Keanu Reeves will each heroically attempt to save the human race from the brutal robot overlords. They will all fail.
Also, I've mentioned Glenn Beck in each of the last two posts (twice in this one if you include the monkey bit). I promise to try not to in the next post.
Wednesday, August 19, 2009
Critical Thinking
I recently came across something in a community college textbook that I found interesting. About three whole pages of this textbook was devoted to giving guidelines for intelligently reading articles of academic interest. I suppose I shouldn't be too surprised, since this is a very important skill to have for those of us in academic fields. However, I don't think there was anything included that any intelligent person shouldn't be able to figure out for himself. Here's roughly what it said:
But when it comes to our roles in mainstream society, there's no reason not to apply these skills to the best of our ability. Take politics, for example:
Do you think Sarah Palin is an expert in health care? What qualifications does she have to decide on issues that affect Americans, besides that time that she ruined McCain's chances of getting elected? How about Glenn Beck? What kind of pedigree is required to make up stuff on TV these days? Unless Glenn Beck is really Dr. Glenn Beck, Phd., it sounds like these two fail the critical thinking check number 1.
Saying that Obama wants to put your grandma to death is a pretty outlandish claim. So are claims that compare proposed health care reform to nazi eugenics. That's check number 2. Upon two failed checks, any sane person should be looking for number 3. Give me a quote from one of the bills (with a page number), and maybe I'll listen. Otherwise, I'd rather spend my time reading up on time cube or flat earth theory. At least those sets of meaningless blabber are moderately entertaining and don't influence the well-being of 47 million people.
Before I get down from my soapbox, I'd like to mention that I really wish I could find better examples from across the aisle. As much as I hate to say it, this isn't a problem with the Republican party, but more just politics in general.
Our political system is one in which "facts" are routinely carefully selected, spun, misinterpreted, or completely fabricated just to back up one's point of view. There isn't a politician alive who doesn't have ulterior motives. They will say whatever they can, just to improve the status of their party, or get a boost in their next campaign. That sounds an awful lot like check number four.
Here's something you can do- read up on the most common logical fallacies, and try to spot them next time you're watching cable news or a debate. Some are so prevalent, that they are named after political phrases that are used when they are committed (like "slippery slope"). Maybe a harder task is to spot an argument that doesn't contain a logical fallacy.
As for check number six, I think you'll agree with me that overgeneralization is not only common in politics, but is an accepted political strategy. For example, taking a thousand-page bill and calling it a "government take-over of health care" is certainly an overgeneralization.
None of these behaviors would be tolerated in any academic field. You wouldn't even tolerate it among your coworkers. Heck, you'd probably scold your kids for some of the same behaviors that are commonplace over on capital hill. And these are the people who are running the country. Go figure.
What's the most frustrating is the fact that this isn't just a big accident. These sorts of deceitful behaviors are nothing but politics-by-design.
Eh. Fuck it.
To be honest, I still don't see why this needs to be outlined in a textbook. After all, in the sciences, these are rules that researchers live or die by. These are things you pick up out of necessity. You either learn to apply them or are subject to ridicule by your peers.
When analyzing the claims that anyone is making, keep the following in mind:
1. Is the writer/speaker an expert in the subject on which he/she is talking about? If not, is there any reason you should trust what this person is saying? (I may be pretty picky, but when it comes to academic matters, an "expert" is someone with an advanced degree in the particular field- at least.)
2. Do the claims disagree with accepted knowledge or are outrageous for other reasons? Such claims are not necessarily false, but there has to be a reason that years of academic pursuit suggest otherwise. (This, usually along with #1, is a primary reason that you can immediately ignore crackpot theorists who make claims like "Quantum Mechanics is obviously wrong" without explaining why quantum mechanics predicts the result of every low-energy experiment ever performed.)
3. Does the writer/speaker provide evidence to support his/her claims? Does the evidence supplied hold up to the same scrutiny? (In academic papers, evidence is shown through the results of individual research, or through citing papers written by other researchers. Seriously- this should be the biggest no-brainer in this list.)
4. Could the writer/speaker have ulterior motives? There are many reasons that a person could make a certain claim, and the pursuit of truth is only one of them. The others include money, social status, political capital, embarrassment, and countless others. Don't be naive.
5. Does the argument contain logical fallacies? Here's a sample of a few:6. Does the claim seem too simple, given the complexity of the subject matter? If someone offers a one-sentence solution to an age-old problem, that usually means that the person ignored a few factors that contributed to the problem in the first place.
- Circular logic
- Correlation implies causation
- Sweeping generalizations
- Bandwagon
- Arguing from ignorance
- Appeals to authority
- Slippery slope
But when it comes to our roles in mainstream society, there's no reason not to apply these skills to the best of our ability. Take politics, for example:
Do you think Sarah Palin is an expert in health care? What qualifications does she have to decide on issues that affect Americans, besides that time that she ruined McCain's chances of getting elected? How about Glenn Beck? What kind of pedigree is required to make up stuff on TV these days? Unless Glenn Beck is really Dr. Glenn Beck, Phd., it sounds like these two fail the critical thinking check number 1.
Saying that Obama wants to put your grandma to death is a pretty outlandish claim. So are claims that compare proposed health care reform to nazi eugenics. That's check number 2. Upon two failed checks, any sane person should be looking for number 3. Give me a quote from one of the bills (with a page number), and maybe I'll listen. Otherwise, I'd rather spend my time reading up on time cube or flat earth theory. At least those sets of meaningless blabber are moderately entertaining and don't influence the well-being of 47 million people.
Before I get down from my soapbox, I'd like to mention that I really wish I could find better examples from across the aisle. As much as I hate to say it, this isn't a problem with the Republican party, but more just politics in general.
Our political system is one in which "facts" are routinely carefully selected, spun, misinterpreted, or completely fabricated just to back up one's point of view. There isn't a politician alive who doesn't have ulterior motives. They will say whatever they can, just to improve the status of their party, or get a boost in their next campaign. That sounds an awful lot like check number four.
Here's something you can do- read up on the most common logical fallacies, and try to spot them next time you're watching cable news or a debate. Some are so prevalent, that they are named after political phrases that are used when they are committed (like "slippery slope"). Maybe a harder task is to spot an argument that doesn't contain a logical fallacy.
As for check number six, I think you'll agree with me that overgeneralization is not only common in politics, but is an accepted political strategy. For example, taking a thousand-page bill and calling it a "government take-over of health care" is certainly an overgeneralization.
None of these behaviors would be tolerated in any academic field. You wouldn't even tolerate it among your coworkers. Heck, you'd probably scold your kids for some of the same behaviors that are commonplace over on capital hill. And these are the people who are running the country. Go figure.
What's the most frustrating is the fact that this isn't just a big accident. These sorts of deceitful behaviors are nothing but politics-by-design.
Eh. Fuck it.
Wednesday, July 29, 2009
Bored?
Here's something fun to do:
Browse the Flat Earth Society Forums and try to figure out which posters are actually serious. In my opinion, some of them must be serious, or else no one would have the energy to maintain that website. On the other hand, I can't believe that they can all believe that the earth is flat. I mean, some of those statements just defy too much reason for someone to actually believe in it. Then again, you just may be surprised.
By the way- I said to browse. Don't bother posting. If you think you have a chance at beating some of these people in a debate, you are quite mistaken. This isn't to say that they have good arguments or really a semblance of coherent thought. There are two specific reasons why you can't beat them in a debate, and here they are:
1. They don't listen to reason. Seriously. How else can you interpret their explanation for those NASA pictures that clearly show an Earth that is circular from all sides? Their answer- a conspiracy. Not only are the governments and scientific communities from all space-able nations involved, but so are satellite TV and GPS companies as well (they actually transmit signals via blimps and radio towers, since satellites are impossible). Those pictures taken from outer space are computer generated- 'cause everyone knows they had photoshop back in the '60s.
Some even claim that there are guards stationed along the ice sheet at the edge of the world to make sure people don't try to go over the edge. Somewhere along the way, you've got to realize that there's something not quite right in the brain with these people here.
2. They can always make up new rules to explain the discrepancies you point out.
Example- why can't you see over the horizon? Answer: Because light follows a curved path while on Earth.
Why does the sun set? Answer: Because the sun (and moon, which gives off its own light) are like spotlights- not isotropic light sources. They only shine on certain parts of the world at a time as they follow circular paths exactly 3000 miles above the surface of the Earth.
How do you explain the phases of the moon? Answer: There is another heavenly body, unknown to mainstream science, which is completely black and at times likes to obscure our view of the moon.
How do you explain gravity on Earth? Answer: There is no gravity on Earth. Instead, a "Dark Energy" continuously accelerates the Earth upward at 9.8 m/s^2. By the way, they do cede that other bodies in space have gravity, thus explaining the existence of tides (but not the fact that there are two tides a day!). As for why other bodies have gravity but not the Earth? Because the Earth is SPECIAL!
Why do distances in the southern hemisphere seem closer than what is suggested by Flat Earth geography? Answer: Remember how the GPS companies are involved in the conspiracy? GPS software intentionally sends planes in paths that make distances in the northern hemisphere seem longer than they really are.
If you come up with something else that's not right with Flat Earth theory, they'll just come up with some other new assumption that would explain the observation. If they can't come up with an explanation, they'll just give the "your a sheep who's been brainwashed by the mainstream scientific conspiracy COME ON PEOPLE WHY DON'T YOU OPEN YOUR EYES!!!" argument.
These two pieces of idiot behavior are a constant among all crackpot pseudo-scientific theories, including null science, autodynamics, intelligent design, and countless others.
I've also observed it among most ardent followers of every religious and political area of thought. Just an observation...
I said most, so don't anyone get mad at me.
Browse the Flat Earth Society Forums and try to figure out which posters are actually serious. In my opinion, some of them must be serious, or else no one would have the energy to maintain that website. On the other hand, I can't believe that they can all believe that the earth is flat. I mean, some of those statements just defy too much reason for someone to actually believe in it. Then again, you just may be surprised.
By the way- I said to browse. Don't bother posting. If you think you have a chance at beating some of these people in a debate, you are quite mistaken. This isn't to say that they have good arguments or really a semblance of coherent thought. There are two specific reasons why you can't beat them in a debate, and here they are:
1. They don't listen to reason. Seriously. How else can you interpret their explanation for those NASA pictures that clearly show an Earth that is circular from all sides? Their answer- a conspiracy. Not only are the governments and scientific communities from all space-able nations involved, but so are satellite TV and GPS companies as well (they actually transmit signals via blimps and radio towers, since satellites are impossible). Those pictures taken from outer space are computer generated- 'cause everyone knows they had photoshop back in the '60s.
Some even claim that there are guards stationed along the ice sheet at the edge of the world to make sure people don't try to go over the edge. Somewhere along the way, you've got to realize that there's something not quite right in the brain with these people here.
2. They can always make up new rules to explain the discrepancies you point out.
Example- why can't you see over the horizon? Answer: Because light follows a curved path while on Earth.
Why does the sun set? Answer: Because the sun (and moon, which gives off its own light) are like spotlights- not isotropic light sources. They only shine on certain parts of the world at a time as they follow circular paths exactly 3000 miles above the surface of the Earth.
How do you explain the phases of the moon? Answer: There is another heavenly body, unknown to mainstream science, which is completely black and at times likes to obscure our view of the moon.
How do you explain gravity on Earth? Answer: There is no gravity on Earth. Instead, a "Dark Energy" continuously accelerates the Earth upward at 9.8 m/s^2. By the way, they do cede that other bodies in space have gravity, thus explaining the existence of tides (but not the fact that there are two tides a day!). As for why other bodies have gravity but not the Earth? Because the Earth is SPECIAL!
Why do distances in the southern hemisphere seem closer than what is suggested by Flat Earth geography? Answer: Remember how the GPS companies are involved in the conspiracy? GPS software intentionally sends planes in paths that make distances in the northern hemisphere seem longer than they really are.
If you come up with something else that's not right with Flat Earth theory, they'll just come up with some other new assumption that would explain the observation. If they can't come up with an explanation, they'll just give the "your a sheep who's been brainwashed by the mainstream scientific conspiracy COME ON PEOPLE WHY DON'T YOU OPEN YOUR EYES!!!" argument.
These two pieces of idiot behavior are a constant among all crackpot pseudo-scientific theories, including null science, autodynamics, intelligent design, and countless others.
I've also observed it among most ardent followers of every religious and political area of thought. Just an observation...
I said most, so don't anyone get mad at me.
Saturday, July 25, 2009
Advertising
--Here's a classic:
"Did you know that 9 out of 10 people need a new mattress?"
Really? What do they sleep on? Two-by-fours? Piles of hay? I didn't think the economy had gotten that bad!
Seriously- what's the criteria for needing a new mattress? I'm pretty sure I do, but that's just because I'm moving to a new apartment. Are 90% of Americans currently relocating? Did their homes just get repossessed?
--"Drivers who switched from Geico to Allstate saved an average of $473."
You think maybe the fact that they saved money had anything to do with the fact that they switched? How many people who switched actually lost money? I have a hunch that number is close to zero, meaning the people who wouldn't have saved weren't included in the sample size. The add may as well say, "Drivers who switched from Geico to Allstate and saved at least $400 saved an average of $473!"
--"Getting the right coverage isn't just about the car, it's about who's in the back seat."
Apparently, car insurance can prevent your kids from getting hurt in a car accident. It's like magic! Oh, wait. No. They just cut you a check and then raise your premiums. Sorry. You'll have to find a witch doctor or something.
--I'm a little tired of fast food commercials where fast food chains try to tell you why their fast food is better than other fast food.
Going to a fast food chain usually isn't one of the best moments of my life. Those moments aren't exactly a good time for brand loyalty. I can't imagine how bad your life has to be in order for you to be particular about your fast food. I just know that the decision of which chain to visit is usually dependent on which one is closest. Then comes the self-hate.
--Around in this area there is a college that airs commercials called 4-D College. First of all, I don't know anything about this college apart from what's on the commercials. Despite this fact, it may very well be a good place to study, but I'm not convinced. So, what does 4-D stand for? No, it's not the average report card of their top students. 4-D stands for the following:
1: Determination
2: Desire
3: Drive
4: Deliver
What? Now, I'm not sure where they make the rules for these mnemonic-driven bullet-point list things, but I'm pretty sure you're not allowed to start it with three nouns and end it with a verb. Plus, the first three are close enough to synonyms to discount the whole list in the first place. Once again, this college may very well be perfectly sufficient in preparing its students for the workplace, but if the commercial is indicative of the education you'll get there...
What I'm just saying is it's usually a good idea to put your best foot forward. And hopefully you've got a good one to show.
"Did you know that 9 out of 10 people need a new mattress?"
Really? What do they sleep on? Two-by-fours? Piles of hay? I didn't think the economy had gotten that bad!
Seriously- what's the criteria for needing a new mattress? I'm pretty sure I do, but that's just because I'm moving to a new apartment. Are 90% of Americans currently relocating? Did their homes just get repossessed?
--"Drivers who switched from Geico to Allstate saved an average of $473."
You think maybe the fact that they saved money had anything to do with the fact that they switched? How many people who switched actually lost money? I have a hunch that number is close to zero, meaning the people who wouldn't have saved weren't included in the sample size. The add may as well say, "Drivers who switched from Geico to Allstate and saved at least $400 saved an average of $473!"
--"Getting the right coverage isn't just about the car, it's about who's in the back seat."
Apparently, car insurance can prevent your kids from getting hurt in a car accident. It's like magic! Oh, wait. No. They just cut you a check and then raise your premiums. Sorry. You'll have to find a witch doctor or something.
--I'm a little tired of fast food commercials where fast food chains try to tell you why their fast food is better than other fast food.
Going to a fast food chain usually isn't one of the best moments of my life. Those moments aren't exactly a good time for brand loyalty. I can't imagine how bad your life has to be in order for you to be particular about your fast food. I just know that the decision of which chain to visit is usually dependent on which one is closest. Then comes the self-hate.
--Around in this area there is a college that airs commercials called 4-D College. First of all, I don't know anything about this college apart from what's on the commercials. Despite this fact, it may very well be a good place to study, but I'm not convinced. So, what does 4-D stand for? No, it's not the average report card of their top students. 4-D stands for the following:
1: Determination
2: Desire
3: Drive
4: Deliver
What? Now, I'm not sure where they make the rules for these mnemonic-driven bullet-point list things, but I'm pretty sure you're not allowed to start it with three nouns and end it with a verb. Plus, the first three are close enough to synonyms to discount the whole list in the first place. Once again, this college may very well be perfectly sufficient in preparing its students for the workplace, but if the commercial is indicative of the education you'll get there...
What I'm just saying is it's usually a good idea to put your best foot forward. And hopefully you've got a good one to show.
Sunday, July 19, 2009
Heisenberg Uncertainty
One of the things that just about everyone knows about quantum mechanics is that it is a theory that only predicts probabilities. In other words, even if you know everything about a particle there is to know, you still may not be able to say where it is. The only thing quantum mechanics can tell you is the probability of detecting the particle in any given location. This fact does not have a famous name, but is often referred to as the indeterminacy of quantum mechanics. What it is not called, however, is the Heisenberg uncertainty principle. I've heard everyone from John Stewart to cult-recruitment movies get this little bit of terminology wrong. This post is about what the Heisenberg uncertainty principle actually is.
The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.
The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.
Wednesday, July 8, 2009
Quantum Mechanics
Quantum Mechanics is one of the most popular yet misunderstood physics topics out there. There are many myths around quantum mechanics that I run into from time to time, and I thought I'd devote some posts to the topic.
Perhaps the biggest myth surrounding quantum mechanics is the idea that it doesn't make sense. This idea is absurd. Quantum mechanics describes how our world works- if it doesn't make sense, then you just don't understand it. Or at least you haven't thought about it in the right way.
Quantum mechanics is baffling yet incredibly simple. You can literally write down all of quantum mechanics on a half-sheet of paper. As a matter of fact, here it is:
- The state of a system is entirely represented by its wave function, which is a unit vector of any number of dimensions (including infinite) existing in Hilbert space. The wave function can be calculated from the Schrodinger equation:
- The expectation value (in a statistical sense) of an observable quantity is the inner product of the wave function with the wave function after being operated on by the observable's hermitian operator.
- Determinate States, or states of a system that correspond to a constant observed value, are eigenstates of the observable's hermitian operator, while the observed value is the eigenvalue. (ex. energy levels that give rise to discrete atomic spectra are eigenvalues corresponding to energy determinate states.)
- All determinate states are orthogonal and all possible states can be expressed as a linear combination of determinate states.
- When a measurement is made, the probability of getting a certain value is the square root of the inner product of that value's determinate state with the wave function.
- Upon measurement, the wave function "collapses", becoming the determinate state corresponding to the value that was measured.
So how bad was that?
Okay, so this is probably confusing to those of you who haven't had a class in quantum mechanics or an advanced course in linear algebra. Getting passed the math, it really isn't that hard conceptually. The important thing to note, though, is the fact that it can be defined so concisely. I think I've actually included more than necessary, so it probably can be even more concise than what I've written. Quantum mechanics is pretty complex in application, but is simple at its core. All of the best theories have this quality.
I'll probably post some stuff later that will (hopefully) clear up some of the details.
Another myth I run into is around the term "Quantum Physicist". There isn't such thing- at least in the professional sense. The reason why is the fact that there isn't a physicist in the world who doesn't use quantum mechanics. If the term "Quantum Physicist" represents a scientist who uses quantum mechanics in his/her research, we can probably just agree to just use the term "Physicist". Likewise, it is impossible to go to college and major in "Quantum Physics". Any respectable university would require its physics majors to learn quantum mechanics, so there is no reason to create a new major around it. I'm saying this in reference to the nerdy characters in movies and TV shows who are described using these terms. If you know anyone who writes screenplays, let them know.
I was going to get into some of the misunderstandings around actual quantum mechanics, but maybe I'll get into it later. Most of these misunderstandings involve the indeterminacy of the statistical interpretation, the Heisenberg uncertainty principle, and the collapse of the wave function. I'll try to get to all these issues later. For now, I'm hungry.
Perhaps the biggest myth surrounding quantum mechanics is the idea that it doesn't make sense. This idea is absurd. Quantum mechanics describes how our world works- if it doesn't make sense, then you just don't understand it. Or at least you haven't thought about it in the right way.
Quantum mechanics is baffling yet incredibly simple. You can literally write down all of quantum mechanics on a half-sheet of paper. As a matter of fact, here it is:
- The state of a system is entirely represented by its wave function, which is a unit vector of any number of dimensions (including infinite) existing in Hilbert space. The wave function can be calculated from the Schrodinger equation:
- The expectation value (in a statistical sense) of an observable quantity is the inner product of the wave function with the wave function after being operated on by the observable's hermitian operator.
- Determinate States, or states of a system that correspond to a constant observed value, are eigenstates of the observable's hermitian operator, while the observed value is the eigenvalue. (ex. energy levels that give rise to discrete atomic spectra are eigenvalues corresponding to energy determinate states.)
- All determinate states are orthogonal and all possible states can be expressed as a linear combination of determinate states.
- When a measurement is made, the probability of getting a certain value is the square root of the inner product of that value's determinate state with the wave function.
- Upon measurement, the wave function "collapses", becoming the determinate state corresponding to the value that was measured.
So how bad was that?
Okay, so this is probably confusing to those of you who haven't had a class in quantum mechanics or an advanced course in linear algebra. Getting passed the math, it really isn't that hard conceptually. The important thing to note, though, is the fact that it can be defined so concisely. I think I've actually included more than necessary, so it probably can be even more concise than what I've written. Quantum mechanics is pretty complex in application, but is simple at its core. All of the best theories have this quality.
I'll probably post some stuff later that will (hopefully) clear up some of the details.
Another myth I run into is around the term "Quantum Physicist". There isn't such thing- at least in the professional sense. The reason why is the fact that there isn't a physicist in the world who doesn't use quantum mechanics. If the term "Quantum Physicist" represents a scientist who uses quantum mechanics in his/her research, we can probably just agree to just use the term "Physicist". Likewise, it is impossible to go to college and major in "Quantum Physics". Any respectable university would require its physics majors to learn quantum mechanics, so there is no reason to create a new major around it. I'm saying this in reference to the nerdy characters in movies and TV shows who are described using these terms. If you know anyone who writes screenplays, let them know.
I was going to get into some of the misunderstandings around actual quantum mechanics, but maybe I'll get into it later. Most of these misunderstandings involve the indeterminacy of the statistical interpretation, the Heisenberg uncertainty principle, and the collapse of the wave function. I'll try to get to all these issues later. For now, I'm hungry.
Tuesday, June 30, 2009
Cartoons
My eight year old brother-in-law's 'Spongebob Squarepants' watching has made me nostalgic for old cartoons of my childhood. If only I could find a single episode of 'loony tunes' on TV somewhere.
But now that 'loony tunes' is off the tube, there are some questions that I find myself asking- like "where are kids these days going to get the introduction to classical music that I had?" 'Loony Tunes' was how kids of my generation got to hear great pieces like Tchaikovsky's "Romeo and Juliet" and Wagner's "Ride of the Valkyrie". Of course, I learned them under the titles "Shot-by-Cupid's-arrow Theme" and "Kill the Wabbit", but I learned them nonetheless. When I just got started listening to classical music, it was nice to hear something familiar. Kids these days don't even recognize these pieces.
Of course, 'loony tunes' is considered by today's standards to be too 'violent'. But to put things in perspective, lets look at a cartoon that is readily watched by kids on TV today called Pokemon.
So, the basic idea behind Pokemon is that a bunch of kids go romping through the woods in search of certain creatures. When they find a creature they want, they beat it up, and trap it inside a tiny ball- where it will stay night and day for just about the remainder of its life. In fact, the only time these creatures are allowed to come out is when they are forced to battle each other for the praise of their owners.
Wow. That sounds like an activity that Micheal Vick would find enjoyable. I'm surprised PETA isn't more involved.
Okay, so maybe my point isn't that clear, but here's what I think: Let's not get into a tizzy fit over what kids watch on TV. Seeing some cartoonish violence isn't nearly as harmful as the effects of being ignored and inactive for long periods of time. Give them attention and something to do with their time, and your kids'll be just fine.
But now that 'loony tunes' is off the tube, there are some questions that I find myself asking- like "where are kids these days going to get the introduction to classical music that I had?" 'Loony Tunes' was how kids of my generation got to hear great pieces like Tchaikovsky's "Romeo and Juliet" and Wagner's "Ride of the Valkyrie". Of course, I learned them under the titles "Shot-by-Cupid's-arrow Theme" and "Kill the Wabbit", but I learned them nonetheless. When I just got started listening to classical music, it was nice to hear something familiar. Kids these days don't even recognize these pieces.
Of course, 'loony tunes' is considered by today's standards to be too 'violent'. But to put things in perspective, lets look at a cartoon that is readily watched by kids on TV today called Pokemon.
So, the basic idea behind Pokemon is that a bunch of kids go romping through the woods in search of certain creatures. When they find a creature they want, they beat it up, and trap it inside a tiny ball- where it will stay night and day for just about the remainder of its life. In fact, the only time these creatures are allowed to come out is when they are forced to battle each other for the praise of their owners.
Wow. That sounds like an activity that Micheal Vick would find enjoyable. I'm surprised PETA isn't more involved.
Okay, so maybe my point isn't that clear, but here's what I think: Let's not get into a tizzy fit over what kids watch on TV. Seeing some cartoonish violence isn't nearly as harmful as the effects of being ignored and inactive for long periods of time. Give them attention and something to do with their time, and your kids'll be just fine.
Tuesday, June 16, 2009
'Fatherhood'
 The next time you know someone who just had his first baby and you want to ask a question like, "so how does it feel to be a father?"- just wait a little while. Wait until after the first few sleepless nights and diaper changes. Maybe he'll have a better idea by then.
The next time you know someone who just had his first baby and you want to ask a question like, "so how does it feel to be a father?"- just wait a little while. Wait until after the first few sleepless nights and diaper changes. Maybe he'll have a better idea by then.The answer: "Tired".
Or maybe you want to ask after the moment that the little stinker opens her eyes and seems to take in her surroundings for the first time. She can only see about a foot in front of her, so she'll gaze at your face incessantly before falling asleep/crying for mommy.
I still don't know how to answer the question in that case. Just look at the picture. See what I'm talking about?
There are some things that I have learned within these first few days with my daughter.
People don't grow up just because they grow older. It's the experiences we have and hardships that we endure that make us better people. People have an amazing ability to live up to expectations. Nowhere are these expectations greater than in the eyes of a child who looks to you for all aspects of her livelihood. Generation after generation of us have risen up to the challenge and everyone has benefited as a result. I suppose it's my turn now.
Wednesday, May 27, 2009
My First Job
I know that everyone has a horror-story first job that they love to complain about (at least those who have worked a day in their lives). People who enjoy their work should consider themselves lucky, and those who have always enjoyed it, well, are probably just out of their minds.
Anyway, my first job was as a bag-boy at Safeway at the age of 16. We were referred to as "Courtesy Clerks", but we all knew we were bag-boys. I made 7.79 an hour, but that eventually went up to 8.39 with a couple "cost of living" pay raises (I guess they didn't know that my cost of living was ZERO).
My responsibilities were to bag groceries, sweep the floors, clean the bathrooms (sorta), and collect carts in the parking lot. Though the cart-collecting was the most physically demanding (especially during those hot summers), I eventually learned to look forward to the hours outside. Why? Because I didn't have to talk to people.
You see, those "courtesy clerks" are told to greet every customer as they bag your groceries. I don't want to point fingers, but this was often pretty difficult due to the fact that most of you don't even seem to notice that the bag-boy is there (I guess those groceries must have bagged themselves!). I basically coped by using the same canned greeting on every customer, like the street performer who only has 30 seconds worth of material (the amount of time it takes to walk past). There was one checker who liked to tease me by using the same greeting on a customer before I could, making me flustered while I try to come up with another greeting before the 2-second window has passed.
After bagging the groceries, I had to ask if the customer needed help out (always- even the body builders buying a loaf of bread). This was even more awkward from the fact that the checkers were also held to the same requirement- meaning, if you don't get offered help to your car TWICE on every trip to the grocery store, then someone isn't doing his job!
Then came the friendly canned "Have a nice day!", and in comes the next customer.
Sweeping was just as bad. Of course, having an hour when you're required to go around the store made it pretty easy to sneak off to the back room and snack on the damaged goods for ten minutes at a time. But then again, there were video cameras in the back room with feeds to the manager's office, so it was hard to get away with it (funny how the cameras are trained on the employees and not potential shoplifters).
And as you can guess, being the "sweeps" person meant you were on call for any spills that occur during your hour (anywhere- including the bathroom, which I won't get into).
But even worse was probably, again, having to talk to customers- saying hello to everyone, answering questions I didn't have answers to, and showing people where certain items were (though my guess was as good as theirs).
Here's my favorite request: "Sorry, there's no more of this item on the shelf. Can you go to the back room and see if there are any back there?"
This is what I'd do: I'd say, "Sure!", go to the back room, count to fifty, come back, shrug and say, "Sorry!".
Seriously- did you think there was another grocery store back there or something? The only products in the back room are produce and beer. Everything else comes in with the shipment late at night and pretty much goes straight to the shelf. The produce is back there because it is literally a full-time job just to wash all of it and keep it stocked in those nice little piles. I'm not sure what the beer is doing. Maybe they need a backup supply to replace all the individual bottles that mysteriously disappear from every other six-pack every Friday and Saturday night (once again- no cameras in the beer aisle as per company policy).
Oh, and for you Coors fans that insist that your beer is "as cold as the rockies" from the moment it's frost-brewed 'till the moment you drink it: The beer isn't refrigerated in the back room. It might be transported in refrigerated trucks, but I'm sure it'll warm up pretty quick sitting there. Don't worry- It'll get cold again once you put it in your fridge. The label will turn blue once its ready.
By the way, that invention is nothing short of pure, essential genius. I mean, how else would you be able to tell whether or not your beer is cold- short of, say, touching it?
Back to Safeway- Probably the worst part of the job was dealing with secret shoppers. Yes, there are people who shop at Safeway, rate the service, and report back to headquarters. The managers get pissed if we got low scores. I know what you're thinking, but no, I don't know where to go to get that job.
When I started at Safeway, the store was averaging about 9.5 out of 10 on every secret shop. Then came a 7. Then a 5. Then a 2. Then we got new managers.
Things never really improved by the time I quit.
I actually got secret-shopped on two occasions. The first time, I got a perfect score- on what's called a GAT. The acronym was used to remind employees to first GREET every customer (Hello!), ANTICIPATE their needs (Can I help you find anything?), and TAKE them to the needed item (Let me show you where it is!).
The managers loved me for about a day, but I had a sneaking suspicion. You see, I don't think I ever successfully pulled off a GAT in all of my time working there. The secret shopper must have misread someone else's nametag, or maybe some other guy named Matt worked there for a day and was transferred away or something.
The other time I was secret shopped, I got a zero. It said that I "walked passed without saying hello or making eye contact". That sounds about right.
Anyways, some good actually did come out of that job. I paid for (most of) my bassoon with that money, and had something to write about for one of my college entrance essays. I think I wrote about how it gave me a reason to go to college- so I wouldn't have to work at an unfulfilling job or some crap like that. I think I made it sound better than what I wrote here.
Maybe I actually did grow up a little there.
Heh...
Anyway, my first job was as a bag-boy at Safeway at the age of 16. We were referred to as "Courtesy Clerks", but we all knew we were bag-boys. I made 7.79 an hour, but that eventually went up to 8.39 with a couple "cost of living" pay raises (I guess they didn't know that my cost of living was ZERO).
My responsibilities were to bag groceries, sweep the floors, clean the bathrooms (sorta), and collect carts in the parking lot. Though the cart-collecting was the most physically demanding (especially during those hot summers), I eventually learned to look forward to the hours outside. Why? Because I didn't have to talk to people.
You see, those "courtesy clerks" are told to greet every customer as they bag your groceries. I don't want to point fingers, but this was often pretty difficult due to the fact that most of you don't even seem to notice that the bag-boy is there (I guess those groceries must have bagged themselves!). I basically coped by using the same canned greeting on every customer, like the street performer who only has 30 seconds worth of material (the amount of time it takes to walk past). There was one checker who liked to tease me by using the same greeting on a customer before I could, making me flustered while I try to come up with another greeting before the 2-second window has passed.
After bagging the groceries, I had to ask if the customer needed help out (always- even the body builders buying a loaf of bread). This was even more awkward from the fact that the checkers were also held to the same requirement- meaning, if you don't get offered help to your car TWICE on every trip to the grocery store, then someone isn't doing his job!
Then came the friendly canned "Have a nice day!", and in comes the next customer.
Sweeping was just as bad. Of course, having an hour when you're required to go around the store made it pretty easy to sneak off to the back room and snack on the damaged goods for ten minutes at a time. But then again, there were video cameras in the back room with feeds to the manager's office, so it was hard to get away with it (funny how the cameras are trained on the employees and not potential shoplifters).
And as you can guess, being the "sweeps" person meant you were on call for any spills that occur during your hour (anywhere- including the bathroom, which I won't get into).
But even worse was probably, again, having to talk to customers- saying hello to everyone, answering questions I didn't have answers to, and showing people where certain items were (though my guess was as good as theirs).
Here's my favorite request: "Sorry, there's no more of this item on the shelf. Can you go to the back room and see if there are any back there?"
This is what I'd do: I'd say, "Sure!", go to the back room, count to fifty, come back, shrug and say, "Sorry!".
Seriously- did you think there was another grocery store back there or something? The only products in the back room are produce and beer. Everything else comes in with the shipment late at night and pretty much goes straight to the shelf. The produce is back there because it is literally a full-time job just to wash all of it and keep it stocked in those nice little piles. I'm not sure what the beer is doing. Maybe they need a backup supply to replace all the individual bottles that mysteriously disappear from every other six-pack every Friday and Saturday night (once again- no cameras in the beer aisle as per company policy).
Oh, and for you Coors fans that insist that your beer is "as cold as the rockies" from the moment it's frost-brewed 'till the moment you drink it: The beer isn't refrigerated in the back room. It might be transported in refrigerated trucks, but I'm sure it'll warm up pretty quick sitting there. Don't worry- It'll get cold again once you put it in your fridge. The label will turn blue once its ready.
By the way, that invention is nothing short of pure, essential genius. I mean, how else would you be able to tell whether or not your beer is cold- short of, say, touching it?
Back to Safeway- Probably the worst part of the job was dealing with secret shoppers. Yes, there are people who shop at Safeway, rate the service, and report back to headquarters. The managers get pissed if we got low scores. I know what you're thinking, but no, I don't know where to go to get that job.
When I started at Safeway, the store was averaging about 9.5 out of 10 on every secret shop. Then came a 7. Then a 5. Then a 2. Then we got new managers.
Things never really improved by the time I quit.
I actually got secret-shopped on two occasions. The first time, I got a perfect score- on what's called a GAT. The acronym was used to remind employees to first GREET every customer (Hello!), ANTICIPATE their needs (Can I help you find anything?), and TAKE them to the needed item (Let me show you where it is!).
The managers loved me for about a day, but I had a sneaking suspicion. You see, I don't think I ever successfully pulled off a GAT in all of my time working there. The secret shopper must have misread someone else's nametag, or maybe some other guy named Matt worked there for a day and was transferred away or something.
The other time I was secret shopped, I got a zero. It said that I "walked passed without saying hello or making eye contact". That sounds about right.
Anyways, some good actually did come out of that job. I paid for (most of) my bassoon with that money, and had something to write about for one of my college entrance essays. I think I wrote about how it gave me a reason to go to college- so I wouldn't have to work at an unfulfilling job or some crap like that. I think I made it sound better than what I wrote here.
Maybe I actually did grow up a little there.
Heh...
'Lost Wages'
Nothing serves as a reminder of the fact that you have grown older quite like when things don't look the same as when you first saw them. Maybe I'm a little young to be talking like this, but it is something that enters my head every time I end up in Las Vegas.
The first time I remember going to Vegas, I was young and on a family vacation visiting relatives, staying at Circus Circus. Maybe it's more my young age at the time than anything else, but I remember how the building seemed to tower above everything else around it. From the hotel room, there was a view of Las Vegas in its entirety- I felt like I was on top of the world.
Ever since then, it seems like there's been a newer, bigger hotel/casino coming up every time I'm back. The old casinos that used to dominate the skyline are diminutive compared to the new ones that sprout up like mushrooms.
The last time I was in Vegas, it was for only a day and hardly to have fun. I looked out the window in the top floor of Treasure Island onto a vastly different sight from that of my childhood. First of all, the view was completely dominated by one building- a gigantic gold-plated behemoth with the word "TRUMP" written in block letters on top. It was like a symbol of Las Vegas excess.
So, here's a question for you: Short men go to the gym to bulk up. Those less endowed in certain areas are apt to buy nice cars. So what sort of secret could possibly be so severe that Donald Trump would require that much compensation?
Anyways, after getting over the daze brought on by the Trump tower, I started to look for other landmarks. And there it was- Circus Circus. It was tiny- like the casino that dwarfs would call 'shrimp'. It could have been your friendly neighborhood mom 'n pop hotel- in a "Drive down main street and take a right after the hardware store" kind of neighborhood. That's how pathetic the building looked compared to the new shiny hotels that litter the skyline.
...Kinda like watching an old, washed-up ballplayer (*cough* Brett Favre).
But Circus Circus was never that great, anyway (threw too many interceptions).
Anyway, back to Vegas- I've seen several articles online within the past few months with titles that go something like, "5 Recession-proof Industries". They talk about industries like health-care which tend to do just as well, or even better when the economy takes a downturn. I wonder if we should add the gambling industry to that list.
Why? Well, maybe the growth of Las Vegas is proof enough. Of course, all those new shiny casinos probably had their finances in order since long before this downturn, but I still don't see how they can continue to fill those rooms. Why would people be so keen on throwing their money away when its already hard to come by? Do they actually expect to MAKE money this way?
Or maybe the casinos are being supported by laid-off wall-street traders who need other avenues to fulfill their gambling fix now that they can't do it at work anymore?
...Just a thought
The first time I remember going to Vegas, I was young and on a family vacation visiting relatives, staying at Circus Circus. Maybe it's more my young age at the time than anything else, but I remember how the building seemed to tower above everything else around it. From the hotel room, there was a view of Las Vegas in its entirety- I felt like I was on top of the world.
Ever since then, it seems like there's been a newer, bigger hotel/casino coming up every time I'm back. The old casinos that used to dominate the skyline are diminutive compared to the new ones that sprout up like mushrooms.
The last time I was in Vegas, it was for only a day and hardly to have fun. I looked out the window in the top floor of Treasure Island onto a vastly different sight from that of my childhood. First of all, the view was completely dominated by one building- a gigantic gold-plated behemoth with the word "TRUMP" written in block letters on top. It was like a symbol of Las Vegas excess.
So, here's a question for you: Short men go to the gym to bulk up. Those less endowed in certain areas are apt to buy nice cars. So what sort of secret could possibly be so severe that Donald Trump would require that much compensation?
Anyways, after getting over the daze brought on by the Trump tower, I started to look for other landmarks. And there it was- Circus Circus. It was tiny- like the casino that dwarfs would call 'shrimp'. It could have been your friendly neighborhood mom 'n pop hotel- in a "Drive down main street and take a right after the hardware store" kind of neighborhood. That's how pathetic the building looked compared to the new shiny hotels that litter the skyline.
...Kinda like watching an old, washed-up ballplayer (*cough* Brett Favre).
But Circus Circus was never that great, anyway (threw too many interceptions).
Anyway, back to Vegas- I've seen several articles online within the past few months with titles that go something like, "5 Recession-proof Industries". They talk about industries like health-care which tend to do just as well, or even better when the economy takes a downturn. I wonder if we should add the gambling industry to that list.
Why? Well, maybe the growth of Las Vegas is proof enough. Of course, all those new shiny casinos probably had their finances in order since long before this downturn, but I still don't see how they can continue to fill those rooms. Why would people be so keen on throwing their money away when its already hard to come by? Do they actually expect to MAKE money this way?
Or maybe the casinos are being supported by laid-off wall-street traders who need other avenues to fulfill their gambling fix now that they can't do it at work anymore?
...Just a thought
Thursday, April 23, 2009
I'm a music snob
Have you seen that e-surance commercial with the guy singing and playing guitar? Well, I've seen it one time too many, and I've decided I'm never EVER going to buy anything from that company, and here's why:
So, the commercial starts with the cartoon guy on a stage, and he starts singing. Next to him is that pink-haired cartoon lady playing the tambourine. In the middle of the commercial, the tambourine goes away for a period of time, and when it comes back, it comes back ON THE WRONG BEATS!!!
By wrong beats, I mean one and three, as opposed to two and four. A jazz drummer mixing up two and four with one and three is enough to turn John Coltrane into Barney the dinosaur. Two and four makes for an uptempo swing. One and three- a polka. Most people might not notice these things, but it drives me crazy.
I once saw a performance on TV of a Bernstein piece titled "Prelude, Fugue, and Rifts" played by some famous European orchestra and conducted by the great Simon Rattle. What I managed to catch while flipping through channels was the "Rifts" section, which was obviously a classical composer's attempt at writing a jazz piece for orchestra. I hated it.
Here's why: What was supposed to be a major orchestra's attempt at playing swing really just turned out to be a bunch of old stodgy Europeans playing triplet rhythms. So whats the difference?... Two and four. Not even Simon Rattle got it right.
Of course, I don't mean that jazz influences don't work in classical music. I think Gershwin was a genius in finding that sweet spot where they blend in just the right way.
I know that I tend to be opinionated on certain matters and that people often disagree with me. I don't like to flaunt my ideas, but I do find a source of pride in having opinions that differ from the mainstream.
For example- I hate Brahms. I don't like to listen to him, nor do I think he's the musical genius that most who study music will say he is. Yes, he has written things that are quite pretty- I would recommend the German Requiem. I just don't think that he has contributed anything groundbreaking; his symphonies are insufferable, and to top it off- his orchestration is appalling. Just listen to some of his contemporaries- like Tchaikovsky, whose music is better in every way. Tchaikovsky was dramatic and original. Brahms was just Beethoven all over again.
I understand that Mozart was a genius, but don't know why anyone would actually enjoy his music today. Mozart's music is leagues ahead of what came before him, but there is music that came after him that sounds so much better.
So, maybe you don't enjoy Stravinsky quite as much as I do. I know that the music I listen to isn't for everyone (maybe just the better ones).
But of course, I'm not the only snob out there when it comes to music. We all think that we could be judges on American Idol. We sit in front of our TV screens in pleasure, watching a group of monkeys perform and beg for the votes that we're not going to give them. We all have our favorites- we cheer them on until the show ends and we don't buy their albums.
But what I love most about music opinions is the fact that we're still allowed to have them and disagree. These days, you can still name off your favorite bands without the fear of someone snapping at your throat. They might disagree or call you a dork, but they still won't angrily recount your conversation to like-minded friends afterward.
But when it comes to politics....
I'm not sure what point I'm trying to make here.
So, the commercial starts with the cartoon guy on a stage, and he starts singing. Next to him is that pink-haired cartoon lady playing the tambourine. In the middle of the commercial, the tambourine goes away for a period of time, and when it comes back, it comes back ON THE WRONG BEATS!!!
By wrong beats, I mean one and three, as opposed to two and four. A jazz drummer mixing up two and four with one and three is enough to turn John Coltrane into Barney the dinosaur. Two and four makes for an uptempo swing. One and three- a polka. Most people might not notice these things, but it drives me crazy.
I once saw a performance on TV of a Bernstein piece titled "Prelude, Fugue, and Rifts" played by some famous European orchestra and conducted by the great Simon Rattle. What I managed to catch while flipping through channels was the "Rifts" section, which was obviously a classical composer's attempt at writing a jazz piece for orchestra. I hated it.
Here's why: What was supposed to be a major orchestra's attempt at playing swing really just turned out to be a bunch of old stodgy Europeans playing triplet rhythms. So whats the difference?... Two and four. Not even Simon Rattle got it right.
Of course, I don't mean that jazz influences don't work in classical music. I think Gershwin was a genius in finding that sweet spot where they blend in just the right way.
I know that I tend to be opinionated on certain matters and that people often disagree with me. I don't like to flaunt my ideas, but I do find a source of pride in having opinions that differ from the mainstream.
For example- I hate Brahms. I don't like to listen to him, nor do I think he's the musical genius that most who study music will say he is. Yes, he has written things that are quite pretty- I would recommend the German Requiem. I just don't think that he has contributed anything groundbreaking; his symphonies are insufferable, and to top it off- his orchestration is appalling. Just listen to some of his contemporaries- like Tchaikovsky, whose music is better in every way. Tchaikovsky was dramatic and original. Brahms was just Beethoven all over again.
I understand that Mozart was a genius, but don't know why anyone would actually enjoy his music today. Mozart's music is leagues ahead of what came before him, but there is music that came after him that sounds so much better.
So, maybe you don't enjoy Stravinsky quite as much as I do. I know that the music I listen to isn't for everyone (maybe just the better ones).
But of course, I'm not the only snob out there when it comes to music. We all think that we could be judges on American Idol. We sit in front of our TV screens in pleasure, watching a group of monkeys perform and beg for the votes that we're not going to give them. We all have our favorites- we cheer them on until the show ends and we don't buy their albums.
But what I love most about music opinions is the fact that we're still allowed to have them and disagree. These days, you can still name off your favorite bands without the fear of someone snapping at your throat. They might disagree or call you a dork, but they still won't angrily recount your conversation to like-minded friends afterward.
But when it comes to politics....
I'm not sure what point I'm trying to make here.
Wednesday, April 15, 2009
Why I (Really) Like Physics (part III)
Energy is a physics concept that has been around forever. Energy conservation is firmly ingrained in the minds of theorists as the one law which has and will never be broken. This simple concept, however, leads to some pretty cool things to think about if you have the time.
Energy is one of those things you learned about if you took a high school or college physics course. You probably learned about it and found that it made many problems easier to solve, but didn't think much of it. Here's a summary of what your physics teacher mentioned:
When you make an object move by imparting a force onto it, you exert work while the object gains energy. We define the amount of energy the object has as the amount of work you had to exert to get it into the state it is in. For example, if you push a cart down the street, it begins to move and attains velocity. The motion of the cart is a form of energy called kinetic energy.
Another example- When you lift up a bowling ball, you are exerting a force on the ball to counteract the force of gravity. The energy gained by the ball is called gravitational potential energy. It is called 'potential' energy because it has the potential to become something else.
For example, if you were to drop that bowling ball, the ball's gravitational potential energy would be converted into kinetic energy, and it suddenly becomes very simple to calculate how fast the ball is traveling the instant before it hits you in the foot.
What we call "conservation of energy" is the thing that makes the concept of energy so useful. The really cool thing about it, however, is that the whole concept of energy really just came about as a mathematical trick- a mathematical trick that turned out to reveal something incredibly profound (another such example would be of entropy, which was used in thermodynamics as a math trick long before people realized it actually represented a physical quantity). Here's a little bit of background in classical mechanics:
In Newtonian mechanics, everything is derived from four assumptions: Newton's three laws of motion, and Newton's law of gravity. The three laws state that: (1) an object in motion stays in motion unless acted upon by a force, (2) force equals mass times acceleration, and (3) when one object exerts a force on another, the second object exerts an equal force on the first in the opposite direction. Newton's law of gravity just establishes the nature of gravitational forces between two massive objects. These four assumptions are a physicist's dream. They are simple and concise, yet describe a huge mess of observations- including Kepler's laws, which had previously gone unexplained for decades.
So, where in these assumptions does energy come in? The answer is it doesn't- at least not explicitly. There's a whole lot of talk about forces, but nothing about energy. Nothing that is, until someone comes along and shows that you can prove (from Newton's laws) that the total energy in a closed system is always constant (that is, so long as there's no friction). In Newtonian mechanics, the concept of energy is purely optional. In principle, you could use Newton's laws to solve for anything you'd like to without the word 'energy' so much as crossing your mind.
Now, lets return to the bowling ball example we went through before. You may have noticed that I intentionally only took the example through to the point right before the bowling ball lands. So let's ask the obvious question now- What happens to the bowling ball's energy after it lands? I think we're in agreement that the bowling ball stops after landing, so its kinetic energy is gone, and it no longer has the potential energy it has before you drop it. Conservation of energy isn't very useful if chunks of energy can suddenly disappear without explanation.
Well, that question was answered by James Joule, a physicist whose work is so essential that the standard unit of energy is named after him. What Joule did that was so important is he forced water through a perforated tube and observed that the temperature of the water increased. He also did a similar experiment by heating water with an electrical energy source. The conclusion that was reached from these experiments was the fact that heat, which was understood to be a substance that made the temperature of objects rise, was really just another form of energy.
So, the answer to our bowling ball crashing to the floor question is this: The bowling ball heats up the floor. Some of the energy also escapes in the form of sound waves, which eventually dissipate by heating up the walls and other objects they bump into. The important thing to notice is the fact that conservation of energy, which was originally our little mathematical trick, is still true in the face of forces that we didn't really consider in the first place.
These forces I'm referring to are called non-conservative forces and include things like friction and wind resistance. The thing that these forces share is that they all create heat. The reason they're called non-conservative is the fact that once energy is converted into heat, it becomes theoretically impossible to convert all of it back into some other form (this is where entropy comes in). This isn't to say that the energy is not conserved- it is only converted to a form that makes it irretrievable.
Now that we've cleared that up, lets look at the bowling ball example from the other way: Where did the energy that raised the bowling ball come from?
Well, the energy that powers your muscles is released in a chemical reaction that converts ATP into ADP. The energy that was used to create the ATP in the first place comes from chemical reactions that convert the food you eat into waste product. The energy stored in food, if you trace it back, originates from photons that travel from the sun and are absorbed in the leaves of plants. I'm sure you all are familiar with the Calorie and all of its stress-inducing properties. But did you know that the Calorie is really just another unit of energy? You could literally take the caloric content of a jelly donut and calculate how many bowling balls you could lift with the energy it provides.
Now, speaking of photons from the sun- the sun gets its energy from the fusion reaction in its core which continuously converts hydrogen into helium, releasing a lot of energy. This reaction has the effect of heating up the star to high temperatures and photons are emitted through blackbody radiation. Just about all sources of energy we use today originate from this blackbody radiation. The exception comes in if you happen to live in an area which is powered by a nuclear reactor. The energy in that case comes from a nuclear reaction involving radioactive isotopes you can find in the soil of your lawn (albeit in tiny quantities).
If you're being really thorough, you might remind yourself that all the energy that powers the sun, as well as your neighborhood nuclear reactor, was released to the universe in the big bang.
To this day, conservation of energy remains one of the few conservation laws that has not been violated, even in the face of other vast changes to physical law. Take, for example, Einstein's relativity. Changes were made to our understanding of energy that you'd never see coming. Formulas like those for kinetic energy had to be completely changed (the speed of light started showing up everywhere!). It turned out that mass was really another form of energy. Despite these changes (or because of them), the basic tenant that the energy of a system is constant remained intact. So many ideas that were firmly ingrained in our minds regarding things like mass, time, and space were thrown away while energy was one of the few that remained.
So, here's another example of something more modern that would seem very strange in Newton's days. A piece of gamma radiation (which is really just a high-energy photon), if it has enough energy, can interact with a nuclear electric field, disappear, and create an electron-positron pair. The electron goes off and does what an electron does, but the positron, which is basically a positively-charged electron, does something that is truly remarkable. The positron bounces around until it loses its kinetic energy, eventually getting trapped in the electric field of an electron. The two particles then annihilate each other, and in their place two gamma rays are emitted in opposite directions.
Care to guess what the energies of these two gamma rays are? Well, if you recall Einstein's mass-energy relation, E = mc^2, you can calculate the rest energy of both the positron and electron, and it happens to be 511 KeV. The energy of the two gamma rays are, not coincidentally, also 511 KeV. The two gamma rays carry off the energy that was released when the electron and positron disappeared.
The example above illustrates what the world of modern particle physics is like. Particles routinely appear and disappear and do other things you wouldn't imagine is possible. Imagine for a second what the world would be like if two baseballs could collide and both subsequently disappear in a huge flash of light. The laws that govern the things we normally see on a daily basis don't apply at the particle level, yet things still follow the basic tenant of conservation of energy, which we knew from Newton's days and didn't need to exist in the first place. Things didn't need to be that way.
As remarkable as the concept of energy is, one might find that it is also a necessary one. After all, the universe would not have any semblance of order unless there was something that was held constant. That 'something' was something we just happened to call "energy".
Energy is one of those things you learned about if you took a high school or college physics course. You probably learned about it and found that it made many problems easier to solve, but didn't think much of it. Here's a summary of what your physics teacher mentioned:
When you make an object move by imparting a force onto it, you exert work while the object gains energy. We define the amount of energy the object has as the amount of work you had to exert to get it into the state it is in. For example, if you push a cart down the street, it begins to move and attains velocity. The motion of the cart is a form of energy called kinetic energy.
Another example- When you lift up a bowling ball, you are exerting a force on the ball to counteract the force of gravity. The energy gained by the ball is called gravitational potential energy. It is called 'potential' energy because it has the potential to become something else.
For example, if you were to drop that bowling ball, the ball's gravitational potential energy would be converted into kinetic energy, and it suddenly becomes very simple to calculate how fast the ball is traveling the instant before it hits you in the foot.
What we call "conservation of energy" is the thing that makes the concept of energy so useful. The really cool thing about it, however, is that the whole concept of energy really just came about as a mathematical trick- a mathematical trick that turned out to reveal something incredibly profound (another such example would be of entropy, which was used in thermodynamics as a math trick long before people realized it actually represented a physical quantity). Here's a little bit of background in classical mechanics:
In Newtonian mechanics, everything is derived from four assumptions: Newton's three laws of motion, and Newton's law of gravity. The three laws state that: (1) an object in motion stays in motion unless acted upon by a force, (2) force equals mass times acceleration, and (3) when one object exerts a force on another, the second object exerts an equal force on the first in the opposite direction. Newton's law of gravity just establishes the nature of gravitational forces between two massive objects. These four assumptions are a physicist's dream. They are simple and concise, yet describe a huge mess of observations- including Kepler's laws, which had previously gone unexplained for decades.
So, where in these assumptions does energy come in? The answer is it doesn't- at least not explicitly. There's a whole lot of talk about forces, but nothing about energy. Nothing that is, until someone comes along and shows that you can prove (from Newton's laws) that the total energy in a closed system is always constant (that is, so long as there's no friction). In Newtonian mechanics, the concept of energy is purely optional. In principle, you could use Newton's laws to solve for anything you'd like to without the word 'energy' so much as crossing your mind.
Now, lets return to the bowling ball example we went through before. You may have noticed that I intentionally only took the example through to the point right before the bowling ball lands. So let's ask the obvious question now- What happens to the bowling ball's energy after it lands? I think we're in agreement that the bowling ball stops after landing, so its kinetic energy is gone, and it no longer has the potential energy it has before you drop it. Conservation of energy isn't very useful if chunks of energy can suddenly disappear without explanation.
Well, that question was answered by James Joule, a physicist whose work is so essential that the standard unit of energy is named after him. What Joule did that was so important is he forced water through a perforated tube and observed that the temperature of the water increased. He also did a similar experiment by heating water with an electrical energy source. The conclusion that was reached from these experiments was the fact that heat, which was understood to be a substance that made the temperature of objects rise, was really just another form of energy.
So, the answer to our bowling ball crashing to the floor question is this: The bowling ball heats up the floor. Some of the energy also escapes in the form of sound waves, which eventually dissipate by heating up the walls and other objects they bump into. The important thing to notice is the fact that conservation of energy, which was originally our little mathematical trick, is still true in the face of forces that we didn't really consider in the first place.
These forces I'm referring to are called non-conservative forces and include things like friction and wind resistance. The thing that these forces share is that they all create heat. The reason they're called non-conservative is the fact that once energy is converted into heat, it becomes theoretically impossible to convert all of it back into some other form (this is where entropy comes in). This isn't to say that the energy is not conserved- it is only converted to a form that makes it irretrievable.
Now that we've cleared that up, lets look at the bowling ball example from the other way: Where did the energy that raised the bowling ball come from?
Well, the energy that powers your muscles is released in a chemical reaction that converts ATP into ADP. The energy that was used to create the ATP in the first place comes from chemical reactions that convert the food you eat into waste product. The energy stored in food, if you trace it back, originates from photons that travel from the sun and are absorbed in the leaves of plants. I'm sure you all are familiar with the Calorie and all of its stress-inducing properties. But did you know that the Calorie is really just another unit of energy? You could literally take the caloric content of a jelly donut and calculate how many bowling balls you could lift with the energy it provides.
Now, speaking of photons from the sun- the sun gets its energy from the fusion reaction in its core which continuously converts hydrogen into helium, releasing a lot of energy. This reaction has the effect of heating up the star to high temperatures and photons are emitted through blackbody radiation. Just about all sources of energy we use today originate from this blackbody radiation. The exception comes in if you happen to live in an area which is powered by a nuclear reactor. The energy in that case comes from a nuclear reaction involving radioactive isotopes you can find in the soil of your lawn (albeit in tiny quantities).
If you're being really thorough, you might remind yourself that all the energy that powers the sun, as well as your neighborhood nuclear reactor, was released to the universe in the big bang.
To this day, conservation of energy remains one of the few conservation laws that has not been violated, even in the face of other vast changes to physical law. Take, for example, Einstein's relativity. Changes were made to our understanding of energy that you'd never see coming. Formulas like those for kinetic energy had to be completely changed (the speed of light started showing up everywhere!). It turned out that mass was really another form of energy. Despite these changes (or because of them), the basic tenant that the energy of a system is constant remained intact. So many ideas that were firmly ingrained in our minds regarding things like mass, time, and space were thrown away while energy was one of the few that remained.
So, here's another example of something more modern that would seem very strange in Newton's days. A piece of gamma radiation (which is really just a high-energy photon), if it has enough energy, can interact with a nuclear electric field, disappear, and create an electron-positron pair. The electron goes off and does what an electron does, but the positron, which is basically a positively-charged electron, does something that is truly remarkable. The positron bounces around until it loses its kinetic energy, eventually getting trapped in the electric field of an electron. The two particles then annihilate each other, and in their place two gamma rays are emitted in opposite directions.
Care to guess what the energies of these two gamma rays are? Well, if you recall Einstein's mass-energy relation, E = mc^2, you can calculate the rest energy of both the positron and electron, and it happens to be 511 KeV. The energy of the two gamma rays are, not coincidentally, also 511 KeV. The two gamma rays carry off the energy that was released when the electron and positron disappeared.
The example above illustrates what the world of modern particle physics is like. Particles routinely appear and disappear and do other things you wouldn't imagine is possible. Imagine for a second what the world would be like if two baseballs could collide and both subsequently disappear in a huge flash of light. The laws that govern the things we normally see on a daily basis don't apply at the particle level, yet things still follow the basic tenant of conservation of energy, which we knew from Newton's days and didn't need to exist in the first place. Things didn't need to be that way.
As remarkable as the concept of energy is, one might find that it is also a necessary one. After all, the universe would not have any semblance of order unless there was something that was held constant. That 'something' was something we just happened to call "energy".
Monday, April 6, 2009
Why I (Actually) Like Physics (part II)
Physics is so friggin' awesome- especially when it gives you an opportunity to go off and play in Santa Barbara for a few years and (hopefully) wait out the recession.
Physics also gives rise to sites like this:
Only physics would give people the opportunity to watch a giant blimp-like object get wheeled through a small town in Germany.
By the way, the blimp-like object in question is a major piece of the KATRIN experiment, which I will probably be a part of come this fall. The purpose of the experiment is to measure the mass of the neutrino.
The neutrino, for those of you who don't know, is an elementary particle that still remains a mystery to physicists in many ways. The fact that we still don't have a clue as to its mass at this point is evidence enough for this claim. The reason we know so little about this particle is that it only interacts via the weak force- or in other words, it hardly interacts with anything. Because a particle has to interact with something before it is detected, this makes the goal of actually detecting these things incredibly hard. There are many experiments today that tackle this immense challenge, but there's something cool about KATRIN that I'd like to mention.
You see, KATRIN will attempt to measure the mass of the neutrino, without actually detecting them!
All the experiment is really going to do is measure the energy spectrum of tritium beta decay electrons. You see, when tritium decays, it produces three products: a Helium-3 nucleus, an electron, and a neutrino. The total energy released in the decay is constant and known, and must be distributed among the three products. As we know from Einstein's mass-energy equivalence, part of this energy must be spent in the creation of the neutrino itself, which makes the distribution of electron energies dependent upon the neutrino's mass.
Of course, the experiment itself isn't THAT simple. Obtaining an energy resolution good enough for the mass range we're probing is no small task, and there is a lot of work being done to make sure all the little things are taken care of.
There's also the possibility that the experiment will produce nothing at all...
But all in all, you must agree that the whole picture is nothing but pure awesome.
Physics also gives rise to sites like this:
Only physics would give people the opportunity to watch a giant blimp-like object get wheeled through a small town in Germany.
By the way, the blimp-like object in question is a major piece of the KATRIN experiment, which I will probably be a part of come this fall. The purpose of the experiment is to measure the mass of the neutrino.
The neutrino, for those of you who don't know, is an elementary particle that still remains a mystery to physicists in many ways. The fact that we still don't have a clue as to its mass at this point is evidence enough for this claim. The reason we know so little about this particle is that it only interacts via the weak force- or in other words, it hardly interacts with anything. Because a particle has to interact with something before it is detected, this makes the goal of actually detecting these things incredibly hard. There are many experiments today that tackle this immense challenge, but there's something cool about KATRIN that I'd like to mention.
You see, KATRIN will attempt to measure the mass of the neutrino, without actually detecting them!
All the experiment is really going to do is measure the energy spectrum of tritium beta decay electrons. You see, when tritium decays, it produces three products: a Helium-3 nucleus, an electron, and a neutrino. The total energy released in the decay is constant and known, and must be distributed among the three products. As we know from Einstein's mass-energy equivalence, part of this energy must be spent in the creation of the neutrino itself, which makes the distribution of electron energies dependent upon the neutrino's mass.
Of course, the experiment itself isn't THAT simple. Obtaining an energy resolution good enough for the mass range we're probing is no small task, and there is a lot of work being done to make sure all the little things are taken care of.
There's also the possibility that the experiment will produce nothing at all...
But all in all, you must agree that the whole picture is nothing but pure awesome.
Friday, March 20, 2009
Risk/Reward
Much has been said of the mistakes that teenagers make. The prevailing idea is that teenagers generally don't think about the consequences of their actions before doing something stupid that gets them in trouble. Studies, however, have shown that not only are teenagers aware of the risks behind their actions, they actually spend a considerable amount of time weighing the risks vs. perceived rewards before finally making their (bad) decision. Here's an example of what might go through their heads:
Action: Going to a party, getting drunk, and driving home afterward.
Risk: Might be grounded/get arrested/kill somebody.
Reward: Social acceptance/pretty popular girl might actually talk to me.
Verdict: Party on!!!
I've observed that this sort of risky behavior may start much earlier than the teenage years. Here's an example from my observations of the three-year old twin boys I talked about in my last post:
During a holiday gathering, these twin boys found themselves standing around a bowl of peanuts and decided to have an extended snack before dinner was served. Not wanting the boys to spoil their appetites, several adults told them to stop eating, yet they still continued, saying, "but I have to eat it!". To get them to stop, their great-grandfather decided to make up a story. He told them that if they ate any more, the big scary dog who was staring in from beyond the sliding glass door would charge in and eat them up.
There was no doubt that the boys believed everything that was said to them. You could see fear in their faces every time they tentatively turned their heads to glance at the dog, assuring themselves that the glass door was securely fastened before turning back around and grabbing more peanuts to put in their mouths. So here's what probably went through their heads:
Action: Eating peanuts.
Risk: Dog might eat me.
Reward: I'd get to eat more peanuts.
Verdict: Eat more peanuts.
Perhaps this sort of risky behavior has a purpose. After all, early man would have had a hard time evolving without taking a few risks. Here's another example:
Action: Forsaking life in a tree and stepping around on the ground.
Risk: Bear might eat me.
Reward: I'd finally get to see what's beyond that bush over there.
Verdict: Walking on four legs is SO last millennium!
Of course, risky behavior will ruin us every now and then. Here's what probably went through the mind of more than one AIG employee:
Action: High-risk credit swap.
Risk: Might default- company loses millions/people lose jobs/economy pulled into downward spiral.
Reward: Company stock goes up by a cent/big bonus.
Verdict: What could possibly go wrong? The government will bail us out if this backfires, anyway.
Action: Going to a party, getting drunk, and driving home afterward.
Risk: Might be grounded/get arrested/kill somebody.
Reward: Social acceptance/pretty popular girl might actually talk to me.
Verdict: Party on!!!
I've observed that this sort of risky behavior may start much earlier than the teenage years. Here's an example from my observations of the three-year old twin boys I talked about in my last post:
During a holiday gathering, these twin boys found themselves standing around a bowl of peanuts and decided to have an extended snack before dinner was served. Not wanting the boys to spoil their appetites, several adults told them to stop eating, yet they still continued, saying, "but I have to eat it!". To get them to stop, their great-grandfather decided to make up a story. He told them that if they ate any more, the big scary dog who was staring in from beyond the sliding glass door would charge in and eat them up.
There was no doubt that the boys believed everything that was said to them. You could see fear in their faces every time they tentatively turned their heads to glance at the dog, assuring themselves that the glass door was securely fastened before turning back around and grabbing more peanuts to put in their mouths. So here's what probably went through their heads:
Action: Eating peanuts.
Risk: Dog might eat me.
Reward: I'd get to eat more peanuts.
Verdict: Eat more peanuts.
Perhaps this sort of risky behavior has a purpose. After all, early man would have had a hard time evolving without taking a few risks. Here's another example:
Action: Forsaking life in a tree and stepping around on the ground.
Risk: Bear might eat me.
Reward: I'd finally get to see what's beyond that bush over there.
Verdict: Walking on four legs is SO last millennium!
Of course, risky behavior will ruin us every now and then. Here's what probably went through the mind of more than one AIG employee:
Action: High-risk credit swap.
Risk: Might default- company loses millions/people lose jobs/economy pulled into downward spiral.
Reward: Company stock goes up by a cent/big bonus.
Verdict: What could possibly go wrong? The government will bail us out if this backfires, anyway.
Kids
Ever since I found out that I'm getting one of my own, I've started to look at those little poop-making troublemakers in a different way. Lately, I've had a few opportunities to observe a pair of 3-year old twin boys. Here are some observations:
1. Kids' personalities really come through early. I didn't expect to see much difference in behavior in these twin boys. Although not identical, they've been subjected to the same developmental conditions since birth, yet they couldn't be farther apart in personality. One is precocious, constantly in search of praise and recognition, and already has a grasp over certain social faux-pas. He watches people with a silent intensity, fascinated by the behaviors and mannerisms of adults, though he clearly still does not understand everything that goes on around him. The other twin gets distracted easily- not by the behavior of people, but by the constant source of puzzles that surround him. He seems to have an instinctual need to put things together in a coherent fashion. He is indifferent to praise and is unembarrassed, though still doesn't like being scolded.
2. I'm not sure whether to call it cute or scary when a 3-year old points a toy gun at you and says: "BANG! Now you're dead!" Admittedly, it does sound much cuter in Chinese than I imagine it would in English.
3. Kids learn everything they know from those around them. This fact should be obvious, but becomes excessively clear when you observe their social interactions- especially when they're upset with people. For example, these twins like to use the same threats that they hear from their parents on a regular basis, such as:
"If you don't stop, we're going to the hospital to get a shot!"
"Keep doing that, and I'm going back to China!"
Those sentences don't sound very threatening from a toddler.
4. Kids believe everything they're told, but are still rebellious. I'll say more on this in my next post.
1. Kids' personalities really come through early. I didn't expect to see much difference in behavior in these twin boys. Although not identical, they've been subjected to the same developmental conditions since birth, yet they couldn't be farther apart in personality. One is precocious, constantly in search of praise and recognition, and already has a grasp over certain social faux-pas. He watches people with a silent intensity, fascinated by the behaviors and mannerisms of adults, though he clearly still does not understand everything that goes on around him. The other twin gets distracted easily- not by the behavior of people, but by the constant source of puzzles that surround him. He seems to have an instinctual need to put things together in a coherent fashion. He is indifferent to praise and is unembarrassed, though still doesn't like being scolded.
2. I'm not sure whether to call it cute or scary when a 3-year old points a toy gun at you and says: "BANG! Now you're dead!" Admittedly, it does sound much cuter in Chinese than I imagine it would in English.
3. Kids learn everything they know from those around them. This fact should be obvious, but becomes excessively clear when you observe their social interactions- especially when they're upset with people. For example, these twins like to use the same threats that they hear from their parents on a regular basis, such as:
"If you don't stop, we're going to the hospital to get a shot!"
"Keep doing that, and I'm going back to China!"
Those sentences don't sound very threatening from a toddler.
4. Kids believe everything they're told, but are still rebellious. I'll say more on this in my next post.
Tuesday, March 10, 2009
I'm a geek
Yes, I am a geek. I'm sure you all knew this fact- especially if you've read some of my earlier posts. I'm aware that the fact that I study physics (and enjoy it) is enough to include me in that category.
Let me share with you the moment that I realized that I was a true geek. I suppose I knew it long before, but this is the first time that the fact really hit home.
The moment came when I was watching the movie Spiderman II. If you're familiar with the story, you know that Spiderman's alter ego, Peter Parker, is also a geek. Now you see, in a movie it's not enough to tell the viewers that Spiderman is a nerd, you have to show it. And what better way to show that the story's superhero is just a supernerd is there than to show him in a lecture hall, completely infatuated with the strange symbols written on the board by an old balding nerd of a professor.
If you saw the movie, this short scene probably made you think, "wow, that guy is a geek!" However, the thought that popped into MY head was, "Hey! We just covered that material last week in Quantum Mechanics!"
Wow! I'm just as nerdy as Spiderman!!!
Now all I need is a radioactive spider....
Of course, not all depictions of geeks in motion pictures are quite as flattering as Spiderman. I must say, however, that I still enjoy watching them- but not for the reasons you might enjoy them.
Let me give another example to illustrate. This one comes from the movie Transformers. I've never actually seen the movie, but a friend told me about this scene and it had me practically rolling on the floor with laughter. The scene goes something like this:
Two nerdy scientists are in a lab, and one turns to the other and says, in a British accent: "Why don't you STOP thinking about Fourier transforms and START thinking about Quantum Mechanics?!"
Now, you might not think that this sentence is particularly funny, but my friend and I both did, and for the same reason. You see, whoever wrote this stupid dialogue obviously has no idea what the terms 'Fourier transform' and 'Quantum Mechanics' even mean. If you are intimately familiar with these two terms, you would know that no scientist sitting in a lab would ever utter that sentence.
This sort of dialogue is the kind that I hear all the time in movies and on tv. It's the kind of dialogue that just screams, "this is the smartest sounding sentence that the writer could come up with".
It just goes to show that while you're making fun of nerds for their lack of athletic ability and social grace, they're probably making fun of you for being an idiot.
Let me share with you the moment that I realized that I was a true geek. I suppose I knew it long before, but this is the first time that the fact really hit home.
The moment came when I was watching the movie Spiderman II. If you're familiar with the story, you know that Spiderman's alter ego, Peter Parker, is also a geek. Now you see, in a movie it's not enough to tell the viewers that Spiderman is a nerd, you have to show it. And what better way to show that the story's superhero is just a supernerd is there than to show him in a lecture hall, completely infatuated with the strange symbols written on the board by an old balding nerd of a professor.
If you saw the movie, this short scene probably made you think, "wow, that guy is a geek!" However, the thought that popped into MY head was, "Hey! We just covered that material last week in Quantum Mechanics!"
Wow! I'm just as nerdy as Spiderman!!!
Now all I need is a radioactive spider....
Of course, not all depictions of geeks in motion pictures are quite as flattering as Spiderman. I must say, however, that I still enjoy watching them- but not for the reasons you might enjoy them.
Let me give another example to illustrate. This one comes from the movie Transformers. I've never actually seen the movie, but a friend told me about this scene and it had me practically rolling on the floor with laughter. The scene goes something like this:
Two nerdy scientists are in a lab, and one turns to the other and says, in a British accent: "Why don't you STOP thinking about Fourier transforms and START thinking about Quantum Mechanics?!"
Now, you might not think that this sentence is particularly funny, but my friend and I both did, and for the same reason. You see, whoever wrote this stupid dialogue obviously has no idea what the terms 'Fourier transform' and 'Quantum Mechanics' even mean. If you are intimately familiar with these two terms, you would know that no scientist sitting in a lab would ever utter that sentence.
This sort of dialogue is the kind that I hear all the time in movies and on tv. It's the kind of dialogue that just screams, "this is the smartest sounding sentence that the writer could come up with".
It just goes to show that while you're making fun of nerds for their lack of athletic ability and social grace, they're probably making fun of you for being an idiot.
Sunday, March 8, 2009
"Political Economics"
There is something in the study of economics that's been bothering me for a bit. Now, I don't claim to really know ANYTHING when it comes to economics, nor have I stepped foot in an economics class or opened an economics textbook since high school. Nevertheless, the subject of today's economy has been too pervasive in the media to ignore, and I've been bothered by a few things I've found troubling- not relating to the economy itself, but by how people deal with it.
Now, let me explain something I've learned about physics research. Physicists always know what to expect from an experiment. That isn't to say that they always know the outcome, since that would make the experiment useless. Physicists use the accepted laws of physics to predict the outcome, and when the outcome does not agree with the laws, they know that something is wrong with the theory. Predicting outcomes is no easy task in today's large-scale experiments, but the standards are just as high. Doing so usually requires the use of sophisticated modeling algorithms and lots of computing power.
Let me give you an example: One professor I talked to at Berkeley gave me a sneak peak at some of the software that was developed for one of the projects in development at the LHC called ATLAS. The ATLAS detector is about the size of a mansion, and the laws that govern the interactions between particles are in no way simple. Nevertheless, software that incorporates all these parameters have been developed since long before the actual detector began construction. Through the computer simulations given from this program, my professor was able to show me exactly what we would see from the detectors, with charts, graphs, and everything you might expect from a large scale experiment. She even showed me the bump on a particular graph that would prove the existence of the Higgs boson. These graphs and charts were made a long time ago, and yet to this day they haven't even started colliding particles at the LHC.
No matter how much a certain experiment costs- from a few thousand to several billion- researchers are held to the same rigorous standards. They must show exactly why the experiment will work, and exactly what the experiment will establish (or no funding!).
Now, to see why I'm a little peeved, let me ask this question: What did Obama do to show that his $3/4 trillion stimulus package would work? All I've heard is a few political sound bites- from both sides of the aisle.
I'm not saying I'm against the package. I'd say I'm cautiously optimistic about it (I voted for Obama, after all). I, however, am concerned with the fact that I've never seen a shred of evidence relating to economic policies. I've heard arguments, but evidence is apparently hard to come by.
I'm aware that economics are quite a bit different from physics. It's definitely harder (maybe impossible) to simulate an economy inside a computer; the variables are uncountable, and people as a whole are unpredictable- even in a statistical sense (that's probably what separates us from animals).
However, economics is a real area of study. People get PhDs in the subject. Papers are published on a regular basis. A Nobel Prize is awarded in economics EVERY YEAR for crying out loud!!! I can't imagine that there isn't a shred of evidence out there that supports the conclusions they make. Why don't they let us see it?
The reason why, I think, is that the people who talk to us about the economy aren't economists- They're politicians. The burden of proof no longer exists when good salesmanship will achieve the same end.
This, coincidentaly, is the other thing I don't like about economics: It's impossible to separate it from the politics that drive it. I can't help but draw a parallel between today's economic theories and the phrase "Christian science". No scientific theory is viable if it is influenced by ideas taken from religious beliefs. In the same way, I won't believe in an economic theory if its purpose is to back up someone's politics.
In other words, I won't believe anyone when they say that tax cuts are the key to fixing the economy. It could be true, but I can't shake the feeling that the theory behind it was just drummed up to get a few more votes. I'm sure there are a lot of smart people with PhDs that can show me exactly why tax cuts will fix the economy, but then again, there are probably smart people with PhDs that will show me exactly why they won't.
And here's another thing: If Nobel prizes are awarded in economics every year, why is it that I haven't heard any new economic ideas in the last decade? I'd use a longer time frame, but I don't think I was politically aware enough more than ten years ago to formulate a comparison.
Maybe my views on economics are merely a result of my ignorance. I'm sure there are those who can prove all of the statements in this post wrong, but you know what? I'd rather hear it from Washington. Then maybe I'd think that those losers actually know something.
Now, let me explain something I've learned about physics research. Physicists always know what to expect from an experiment. That isn't to say that they always know the outcome, since that would make the experiment useless. Physicists use the accepted laws of physics to predict the outcome, and when the outcome does not agree with the laws, they know that something is wrong with the theory. Predicting outcomes is no easy task in today's large-scale experiments, but the standards are just as high. Doing so usually requires the use of sophisticated modeling algorithms and lots of computing power.
Let me give you an example: One professor I talked to at Berkeley gave me a sneak peak at some of the software that was developed for one of the projects in development at the LHC called ATLAS. The ATLAS detector is about the size of a mansion, and the laws that govern the interactions between particles are in no way simple. Nevertheless, software that incorporates all these parameters have been developed since long before the actual detector began construction. Through the computer simulations given from this program, my professor was able to show me exactly what we would see from the detectors, with charts, graphs, and everything you might expect from a large scale experiment. She even showed me the bump on a particular graph that would prove the existence of the Higgs boson. These graphs and charts were made a long time ago, and yet to this day they haven't even started colliding particles at the LHC.
No matter how much a certain experiment costs- from a few thousand to several billion- researchers are held to the same rigorous standards. They must show exactly why the experiment will work, and exactly what the experiment will establish (or no funding!).
Now, to see why I'm a little peeved, let me ask this question: What did Obama do to show that his $3/4 trillion stimulus package would work? All I've heard is a few political sound bites- from both sides of the aisle.
I'm not saying I'm against the package. I'd say I'm cautiously optimistic about it (I voted for Obama, after all). I, however, am concerned with the fact that I've never seen a shred of evidence relating to economic policies. I've heard arguments, but evidence is apparently hard to come by.
I'm aware that economics are quite a bit different from physics. It's definitely harder (maybe impossible) to simulate an economy inside a computer; the variables are uncountable, and people as a whole are unpredictable- even in a statistical sense (that's probably what separates us from animals).
However, economics is a real area of study. People get PhDs in the subject. Papers are published on a regular basis. A Nobel Prize is awarded in economics EVERY YEAR for crying out loud!!! I can't imagine that there isn't a shred of evidence out there that supports the conclusions they make. Why don't they let us see it?
The reason why, I think, is that the people who talk to us about the economy aren't economists- They're politicians. The burden of proof no longer exists when good salesmanship will achieve the same end.
This, coincidentaly, is the other thing I don't like about economics: It's impossible to separate it from the politics that drive it. I can't help but draw a parallel between today's economic theories and the phrase "Christian science". No scientific theory is viable if it is influenced by ideas taken from religious beliefs. In the same way, I won't believe in an economic theory if its purpose is to back up someone's politics.
In other words, I won't believe anyone when they say that tax cuts are the key to fixing the economy. It could be true, but I can't shake the feeling that the theory behind it was just drummed up to get a few more votes. I'm sure there are a lot of smart people with PhDs that can show me exactly why tax cuts will fix the economy, but then again, there are probably smart people with PhDs that will show me exactly why they won't.
And here's another thing: If Nobel prizes are awarded in economics every year, why is it that I haven't heard any new economic ideas in the last decade? I'd use a longer time frame, but I don't think I was politically aware enough more than ten years ago to formulate a comparison.
Maybe my views on economics are merely a result of my ignorance. I'm sure there are those who can prove all of the statements in this post wrong, but you know what? I'd rather hear it from Washington. Then maybe I'd think that those losers actually know something.
Saturday, February 21, 2009
'Math Tutor'
I'm currently working as a math tutor. I can't say I'm the best at what I'm doing, but I think I have one thing to brag about to others who have tutored in the past.
You see, there are some people who can teach a kindergartener how to add and subtract. Other people are good at teaching higher maths like calculus to high schoolers.
I, on the other hand, have done both......AT THE SAME TIME!!
Imagine this: I'm sitting at a table in collared shirt and tie. Across from me to the left is just about the cutest 5-year old girl you've ever seen, working on addition and subtraction problems I made up for her. To the right is an 11th grader doing calculus problems. Here's a sample interaction:
".....so, if there are three frogs on a log and two more hop on, NOW how many do you have?"
".....five?"
"GOOD!!!! Now, can you work on these next few problems?"
"...ok....."
(turn)
"Alright, so.....To do this integral, it's probably easiest to use this substitution....."
The place where I work likes to do individualized tutoring, but keeps the cost down by having up to three students per tutor at a time. Tutors are supposed to keep the kids busy by assigning problems during the class period and dividing up the one-on-one time. As you can imagine, it's not usually that simple.
One thing I found strange is that they specifically asked whether I was more comfortable teaching math or verbal, but never asked about what age groups I was comfortable with.
Well, I suppose they did ask me if I could teach kids, but it was after they hired me, and besides, what was I supposed to say?
...Not that I'm bad with kids or anything.
You see, there are some people who can teach a kindergartener how to add and subtract. Other people are good at teaching higher maths like calculus to high schoolers.
I, on the other hand, have done both......AT THE SAME TIME!!
Imagine this: I'm sitting at a table in collared shirt and tie. Across from me to the left is just about the cutest 5-year old girl you've ever seen, working on addition and subtraction problems I made up for her. To the right is an 11th grader doing calculus problems. Here's a sample interaction:
".....so, if there are three frogs on a log and two more hop on, NOW how many do you have?"
".....five?"
"GOOD!!!! Now, can you work on these next few problems?"
"...ok....."
(turn)
"Alright, so.....To do this integral, it's probably easiest to use this substitution....."
The place where I work likes to do individualized tutoring, but keeps the cost down by having up to three students per tutor at a time. Tutors are supposed to keep the kids busy by assigning problems during the class period and dividing up the one-on-one time. As you can imagine, it's not usually that simple.
One thing I found strange is that they specifically asked whether I was more comfortable teaching math or verbal, but never asked about what age groups I was comfortable with.
Well, I suppose they did ask me if I could teach kids, but it was after they hired me, and besides, what was I supposed to say?
...Not that I'm bad with kids or anything.
Wednesday, February 18, 2009
Story
Here's a story.
Once upon a time, there was an 'organization'. This 'organization' was doing very 'well'. 'Investors' of the organization were happy. The organization was making 'lots' of 'money'.
There came a time, however, when 'members' of the organization started 'implementing' 'practices' that would one day threaten the organization. For a time, these 'practices' made the organization do even better. 'Investors' were happy. The organization was making 'lots' of 'money'.
There were several people, other 'members' of the organization, who became aware of these 'practices'. These people took it upon themselves to warn the 'higher-ups' in the organization of these adverse 'practices'. These 'practices', they said, would one day threaten the organization. 'Investors' would be angry. The senate would have hearings. 60 Minutes would do stories.
But the 'higher-ups' of the organization said that there is nothing wrong. After all, the organization is doing 'well'. 'Investors' are happy. The organization is making 'lots' of 'money'.
But there came a time when the 'practices' did, indeed come to threaten the organization. 'Investors' got angry. The senate had hearings. 60 Minutes did stories.
And everyone wondered why the 'higher-ups' did not heed the warnings they had been given. The 'higher-ups' claimed that they were not at fault. They had no reason to do anything about the 'practices' that eventually threatened the organization. After all, at the time, the organization was doing 'well'. 'Investors' were happy, and they were making 'lots' of 'money'.
THE END
So, my astute readers- what is the story about?
The mortgage crisis....
or Major League Baseball?
Once upon a time, there was an 'organization'. This 'organization' was doing very 'well'. 'Investors' of the organization were happy. The organization was making 'lots' of 'money'.
There came a time, however, when 'members' of the organization started 'implementing' 'practices' that would one day threaten the organization. For a time, these 'practices' made the organization do even better. 'Investors' were happy. The organization was making 'lots' of 'money'.
There were several people, other 'members' of the organization, who became aware of these 'practices'. These people took it upon themselves to warn the 'higher-ups' in the organization of these adverse 'practices'. These 'practices', they said, would one day threaten the organization. 'Investors' would be angry. The senate would have hearings. 60 Minutes would do stories.
But the 'higher-ups' of the organization said that there is nothing wrong. After all, the organization is doing 'well'. 'Investors' are happy. The organization is making 'lots' of 'money'.
But there came a time when the 'practices' did, indeed come to threaten the organization. 'Investors' got angry. The senate had hearings. 60 Minutes did stories.
And everyone wondered why the 'higher-ups' did not heed the warnings they had been given. The 'higher-ups' claimed that they were not at fault. They had no reason to do anything about the 'practices' that eventually threatened the organization. After all, at the time, the organization was doing 'well'. 'Investors' were happy, and they were making 'lots' of 'money'.
THE END
So, my astute readers- what is the story about?
The mortgage crisis....
or Major League Baseball?
Tuesday, February 17, 2009
Why I (actually) like physics (part I)
I'm not sure how many parts there will be, but I don't think this post will say everything I'd like to. To follow is just one example that I hope illustrates what it is I like about physics.
I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...
I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:
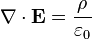

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...
Subscribe to:
Posts (Atom)