I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:
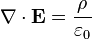
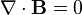
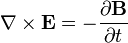

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...

Matt, this is so cool. You can be the next Brian Green. I'm serious.
ReplyDeleteMatt, you just blew my mind SO hard.
ReplyDelete