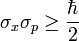Here's something fun to do:
Browse the Flat Earth Society Forums and try to figure out which posters are actually serious. In my opinion, some of them must be serious, or else no one would have the energy to maintain that website. On the other hand, I can't believe that they can all believe that the earth is flat. I mean, some of those statements just defy too much reason for someone to actually believe in it. Then again, you just may be surprised.
By the way- I said to browse. Don't bother posting. If you think you have a chance at beating some of these people in a debate, you are quite mistaken. This isn't to say that they have good arguments or really a semblance of coherent thought. There are two specific reasons why you can't beat them in a debate, and here they are:
1. They don't listen to reason. Seriously. How else can you interpret their explanation for those NASA pictures that clearly show an Earth that is circular from all sides? Their answer- a conspiracy. Not only are the governments and scientific communities from all space-able nations involved, but so are satellite TV and GPS companies as well (they actually transmit signals via blimps and radio towers, since satellites are impossible). Those pictures taken from outer space are computer generated- 'cause everyone knows they had photoshop back in the '60s.
Some even claim that there are guards stationed along the ice sheet at the edge of the world to make sure people don't try to go over the edge. Somewhere along the way, you've got to realize that there's something not quite right in the brain with these people here.
2. They can always make up new rules to explain the discrepancies you point out.
Example- why can't you see over the horizon? Answer: Because light follows a curved path while on Earth.
Why does the sun set? Answer: Because the sun (and moon, which gives off its own light) are like spotlights- not isotropic light sources. They only shine on certain parts of the world at a time as they follow circular paths exactly 3000 miles above the surface of the Earth.
How do you explain the phases of the moon? Answer: There is another heavenly body, unknown to mainstream science, which is completely black and at times likes to obscure our view of the moon.
How do you explain gravity on Earth? Answer: There is no gravity on Earth. Instead, a "Dark Energy" continuously accelerates the Earth upward at 9.8 m/s^2. By the way, they do cede that other bodies in space have gravity, thus explaining the existence of tides (but not the fact that there are two tides a day!). As for why other bodies have gravity but not the Earth? Because the Earth is SPECIAL!
Why do distances in the southern hemisphere seem closer than what is suggested by Flat Earth geography? Answer: Remember how the GPS companies are involved in the conspiracy? GPS software intentionally sends planes in paths that make distances in the northern hemisphere seem longer than they really are.
If you come up with something else that's not right with Flat Earth theory, they'll just come up with some other new assumption that would explain the observation. If they can't come up with an explanation, they'll just give the "your a sheep who's been brainwashed by the mainstream scientific conspiracy COME ON PEOPLE WHY DON'T YOU OPEN YOUR EYES!!!" argument.
These two pieces of idiot behavior are a constant among all crackpot pseudo-scientific theories, including null science, autodynamics, intelligent design, and countless others.
I've also observed it among most ardent followers of every religious and political area of thought. Just an observation...
I said most, so don't anyone get mad at me.
Wednesday, July 29, 2009
Saturday, July 25, 2009
Advertising
--Here's a classic:
"Did you know that 9 out of 10 people need a new mattress?"
Really? What do they sleep on? Two-by-fours? Piles of hay? I didn't think the economy had gotten that bad!
Seriously- what's the criteria for needing a new mattress? I'm pretty sure I do, but that's just because I'm moving to a new apartment. Are 90% of Americans currently relocating? Did their homes just get repossessed?
--"Drivers who switched from Geico to Allstate saved an average of $473."
You think maybe the fact that they saved money had anything to do with the fact that they switched? How many people who switched actually lost money? I have a hunch that number is close to zero, meaning the people who wouldn't have saved weren't included in the sample size. The add may as well say, "Drivers who switched from Geico to Allstate and saved at least $400 saved an average of $473!"
--"Getting the right coverage isn't just about the car, it's about who's in the back seat."
Apparently, car insurance can prevent your kids from getting hurt in a car accident. It's like magic! Oh, wait. No. They just cut you a check and then raise your premiums. Sorry. You'll have to find a witch doctor or something.
--I'm a little tired of fast food commercials where fast food chains try to tell you why their fast food is better than other fast food.
Going to a fast food chain usually isn't one of the best moments of my life. Those moments aren't exactly a good time for brand loyalty. I can't imagine how bad your life has to be in order for you to be particular about your fast food. I just know that the decision of which chain to visit is usually dependent on which one is closest. Then comes the self-hate.
--Around in this area there is a college that airs commercials called 4-D College. First of all, I don't know anything about this college apart from what's on the commercials. Despite this fact, it may very well be a good place to study, but I'm not convinced. So, what does 4-D stand for? No, it's not the average report card of their top students. 4-D stands for the following:
1: Determination
2: Desire
3: Drive
4: Deliver
What? Now, I'm not sure where they make the rules for these mnemonic-driven bullet-point list things, but I'm pretty sure you're not allowed to start it with three nouns and end it with a verb. Plus, the first three are close enough to synonyms to discount the whole list in the first place. Once again, this college may very well be perfectly sufficient in preparing its students for the workplace, but if the commercial is indicative of the education you'll get there...
What I'm just saying is it's usually a good idea to put your best foot forward. And hopefully you've got a good one to show.
"Did you know that 9 out of 10 people need a new mattress?"
Really? What do they sleep on? Two-by-fours? Piles of hay? I didn't think the economy had gotten that bad!
Seriously- what's the criteria for needing a new mattress? I'm pretty sure I do, but that's just because I'm moving to a new apartment. Are 90% of Americans currently relocating? Did their homes just get repossessed?
--"Drivers who switched from Geico to Allstate saved an average of $473."
You think maybe the fact that they saved money had anything to do with the fact that they switched? How many people who switched actually lost money? I have a hunch that number is close to zero, meaning the people who wouldn't have saved weren't included in the sample size. The add may as well say, "Drivers who switched from Geico to Allstate and saved at least $400 saved an average of $473!"
--"Getting the right coverage isn't just about the car, it's about who's in the back seat."
Apparently, car insurance can prevent your kids from getting hurt in a car accident. It's like magic! Oh, wait. No. They just cut you a check and then raise your premiums. Sorry. You'll have to find a witch doctor or something.
--I'm a little tired of fast food commercials where fast food chains try to tell you why their fast food is better than other fast food.
Going to a fast food chain usually isn't one of the best moments of my life. Those moments aren't exactly a good time for brand loyalty. I can't imagine how bad your life has to be in order for you to be particular about your fast food. I just know that the decision of which chain to visit is usually dependent on which one is closest. Then comes the self-hate.
--Around in this area there is a college that airs commercials called 4-D College. First of all, I don't know anything about this college apart from what's on the commercials. Despite this fact, it may very well be a good place to study, but I'm not convinced. So, what does 4-D stand for? No, it's not the average report card of their top students. 4-D stands for the following:
1: Determination
2: Desire
3: Drive
4: Deliver
What? Now, I'm not sure where they make the rules for these mnemonic-driven bullet-point list things, but I'm pretty sure you're not allowed to start it with three nouns and end it with a verb. Plus, the first three are close enough to synonyms to discount the whole list in the first place. Once again, this college may very well be perfectly sufficient in preparing its students for the workplace, but if the commercial is indicative of the education you'll get there...
What I'm just saying is it's usually a good idea to put your best foot forward. And hopefully you've got a good one to show.
Sunday, July 19, 2009
Heisenberg Uncertainty
One of the things that just about everyone knows about quantum mechanics is that it is a theory that only predicts probabilities. In other words, even if you know everything about a particle there is to know, you still may not be able to say where it is. The only thing quantum mechanics can tell you is the probability of detecting the particle in any given location. This fact does not have a famous name, but is often referred to as the indeterminacy of quantum mechanics. What it is not called, however, is the Heisenberg uncertainty principle. I've heard everyone from John Stewart to cult-recruitment movies get this little bit of terminology wrong. This post is about what the Heisenberg uncertainty principle actually is.
The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.
The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.
Wednesday, July 8, 2009
Quantum Mechanics
Quantum Mechanics is one of the most popular yet misunderstood physics topics out there. There are many myths around quantum mechanics that I run into from time to time, and I thought I'd devote some posts to the topic.
Perhaps the biggest myth surrounding quantum mechanics is the idea that it doesn't make sense. This idea is absurd. Quantum mechanics describes how our world works- if it doesn't make sense, then you just don't understand it. Or at least you haven't thought about it in the right way.
Quantum mechanics is baffling yet incredibly simple. You can literally write down all of quantum mechanics on a half-sheet of paper. As a matter of fact, here it is:
- The state of a system is entirely represented by its wave function, which is a unit vector of any number of dimensions (including infinite) existing in Hilbert space. The wave function can be calculated from the Schrodinger equation:
- The expectation value (in a statistical sense) of an observable quantity is the inner product of the wave function with the wave function after being operated on by the observable's hermitian operator.
- Determinate States, or states of a system that correspond to a constant observed value, are eigenstates of the observable's hermitian operator, while the observed value is the eigenvalue. (ex. energy levels that give rise to discrete atomic spectra are eigenvalues corresponding to energy determinate states.)
- All determinate states are orthogonal and all possible states can be expressed as a linear combination of determinate states.
- When a measurement is made, the probability of getting a certain value is the square root of the inner product of that value's determinate state with the wave function.
- Upon measurement, the wave function "collapses", becoming the determinate state corresponding to the value that was measured.
So how bad was that?
Okay, so this is probably confusing to those of you who haven't had a class in quantum mechanics or an advanced course in linear algebra. Getting passed the math, it really isn't that hard conceptually. The important thing to note, though, is the fact that it can be defined so concisely. I think I've actually included more than necessary, so it probably can be even more concise than what I've written. Quantum mechanics is pretty complex in application, but is simple at its core. All of the best theories have this quality.
I'll probably post some stuff later that will (hopefully) clear up some of the details.
Another myth I run into is around the term "Quantum Physicist". There isn't such thing- at least in the professional sense. The reason why is the fact that there isn't a physicist in the world who doesn't use quantum mechanics. If the term "Quantum Physicist" represents a scientist who uses quantum mechanics in his/her research, we can probably just agree to just use the term "Physicist". Likewise, it is impossible to go to college and major in "Quantum Physics". Any respectable university would require its physics majors to learn quantum mechanics, so there is no reason to create a new major around it. I'm saying this in reference to the nerdy characters in movies and TV shows who are described using these terms. If you know anyone who writes screenplays, let them know.
I was going to get into some of the misunderstandings around actual quantum mechanics, but maybe I'll get into it later. Most of these misunderstandings involve the indeterminacy of the statistical interpretation, the Heisenberg uncertainty principle, and the collapse of the wave function. I'll try to get to all these issues later. For now, I'm hungry.
Perhaps the biggest myth surrounding quantum mechanics is the idea that it doesn't make sense. This idea is absurd. Quantum mechanics describes how our world works- if it doesn't make sense, then you just don't understand it. Or at least you haven't thought about it in the right way.
Quantum mechanics is baffling yet incredibly simple. You can literally write down all of quantum mechanics on a half-sheet of paper. As a matter of fact, here it is:
- The state of a system is entirely represented by its wave function, which is a unit vector of any number of dimensions (including infinite) existing in Hilbert space. The wave function can be calculated from the Schrodinger equation:
- The expectation value (in a statistical sense) of an observable quantity is the inner product of the wave function with the wave function after being operated on by the observable's hermitian operator.
- Determinate States, or states of a system that correspond to a constant observed value, are eigenstates of the observable's hermitian operator, while the observed value is the eigenvalue. (ex. energy levels that give rise to discrete atomic spectra are eigenvalues corresponding to energy determinate states.)
- All determinate states are orthogonal and all possible states can be expressed as a linear combination of determinate states.
- When a measurement is made, the probability of getting a certain value is the square root of the inner product of that value's determinate state with the wave function.
- Upon measurement, the wave function "collapses", becoming the determinate state corresponding to the value that was measured.
So how bad was that?
Okay, so this is probably confusing to those of you who haven't had a class in quantum mechanics or an advanced course in linear algebra. Getting passed the math, it really isn't that hard conceptually. The important thing to note, though, is the fact that it can be defined so concisely. I think I've actually included more than necessary, so it probably can be even more concise than what I've written. Quantum mechanics is pretty complex in application, but is simple at its core. All of the best theories have this quality.
I'll probably post some stuff later that will (hopefully) clear up some of the details.
Another myth I run into is around the term "Quantum Physicist". There isn't such thing- at least in the professional sense. The reason why is the fact that there isn't a physicist in the world who doesn't use quantum mechanics. If the term "Quantum Physicist" represents a scientist who uses quantum mechanics in his/her research, we can probably just agree to just use the term "Physicist". Likewise, it is impossible to go to college and major in "Quantum Physics". Any respectable university would require its physics majors to learn quantum mechanics, so there is no reason to create a new major around it. I'm saying this in reference to the nerdy characters in movies and TV shows who are described using these terms. If you know anyone who writes screenplays, let them know.
I was going to get into some of the misunderstandings around actual quantum mechanics, but maybe I'll get into it later. Most of these misunderstandings involve the indeterminacy of the statistical interpretation, the Heisenberg uncertainty principle, and the collapse of the wave function. I'll try to get to all these issues later. For now, I'm hungry.
Subscribe to:
Posts (Atom)