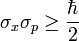So, the LHC is up and running, and has finally begun producing collisions! Seventh and Eighth-year high energy physics graduate students are celebrating (and working hard) around the world at the prospect that they might actually get their PhDs after all!
Oh, and the world hasn't been destroyed yet! For those of you who are still worried by the thought that the LHC will create a black hole and collapse the Earth in on itself, here's a web site with up-to-date information:
Has the large hadron collider destroyed the world yet?
Showing posts with label Physics. Show all posts
Showing posts with label Physics. Show all posts
Saturday, December 5, 2009
Sunday, November 1, 2009
Physicists are Everywhere
For those of you who don't really know what goes on in the world of experimental physics, let me tell you about what I've been doing the last couple weeks.
So, I've posted about the KATRIN project before, but here's a recap: KATRIN is a project that aims to directly measure the neutrino mass by examining the beta-decay spectrum of tritium. The specific part I'm working on is the rear section, which is an important calibration piece of the experiment. For the output of the experiment to make sense, we need to know precisely how much tritium there is in the system at any given time. To accomplish this, we use a detector in the back wall to count the electrons that don't make it through the main spectrometer.
Now, I've been examining one potential problem with this picture- one having to do with electron scattering. You see, the beta decay electrons don't just travel around until they hit the detector- they can also scatter by interacting with the tritium in the column. These interactions make the electrons lose energy, and happen with more frequency when the tritium density increases. With less energy, the electrons are then less likely to be counted in the back end, and this introduces a systematic uncertainty into the measurement of the tritium density.
So, to explore the problem, I wrote a monte carlo program that shows the effect that electron scattering actually has. My program first randomly selects where the electron is emitted from, and at which angle. Then the program selects how far it gets before it scatters, and how much energy it loses. If the electron hasn't reached the wall, the process repeats until it does. Then, the program repeats the whole process again until it has simulated 100,000 electrons. Then, I ran my output through my professor's code, which does a similar thing with the detector design we're using. Altogether, these simulations show what we should expect as an output, should we see some variation in the tritium density, and gives a baseline for the systematic uncertainties we should expect. It also gives us some commentary on the feasibility of the detector design.
I have a point, but you'll have to read on.
At the beginning of baseball season every year, you can usually find some article online talking about computer algorithms that predict the outcomes of the coming season. These algorithms calculate how many games a team will win, how many runs they will score, their likelihood of making the playoffs, and much more. The way they do it is actually quite simple (in principle).
These algorithms merely take the rosters of each team, and uses each players' projected stats to calculate the likelihood of every possible outcome of any particular pitcher-batter match-up. Using these stats, the algorithms simulate every game of the season, one plate appearance at a time. They then repeat the algorithm about a thousand times to minimize uncertainties in random variations.
Hopefully you're starting to see a pattern. Here's another example:
Last fall, I watched a few episodes of a show called "Deadliest Warrior". The premise of the show is that they explore and analyze the weapons and fighting techniques of some of history's most famous warriors, and try to answer the question of who was more lethal. It's the perfect show for any guy who has ever sat around drinking with his buddies and asked the question, "Hey, if a samurai and a viking ever fought to the death, who would win?" The answer, of course- the samurai.
Anyway, so here's how the show went about answering this question: First, they invited experts and martial artists to showcase the weapons and techniques of each side, running tests on each weapon to determine its killing ability. Then, they put the data into a computer program that simulated the battle, blow by blow, a thousand times and tallied the wins for each side.
I'm not an expert in financial markets, but I'm pretty sure they do something similar there as well.
So, maybe my point is this: The work that goes on in the Physics world doesn't need to seem so distant and scary. There are many people out there who do very similar work in fields that are much more accessible to the general public.
As a matter of fact, my job is much easier than those that I highlighted earlier. My program is about 100 lines of Python code. Sports and battle simulations are much harder to do.
For example, those computer algorithms seem to predict the Yankees winning the world series every year. This year is the first since 2000 that they've been right.
...And I think we know what kind of track record the banking industry has...
So, I've posted about the KATRIN project before, but here's a recap: KATRIN is a project that aims to directly measure the neutrino mass by examining the beta-decay spectrum of tritium. The specific part I'm working on is the rear section, which is an important calibration piece of the experiment. For the output of the experiment to make sense, we need to know precisely how much tritium there is in the system at any given time. To accomplish this, we use a detector in the back wall to count the electrons that don't make it through the main spectrometer.
Now, I've been examining one potential problem with this picture- one having to do with electron scattering. You see, the beta decay electrons don't just travel around until they hit the detector- they can also scatter by interacting with the tritium in the column. These interactions make the electrons lose energy, and happen with more frequency when the tritium density increases. With less energy, the electrons are then less likely to be counted in the back end, and this introduces a systematic uncertainty into the measurement of the tritium density.
So, to explore the problem, I wrote a monte carlo program that shows the effect that electron scattering actually has. My program first randomly selects where the electron is emitted from, and at which angle. Then the program selects how far it gets before it scatters, and how much energy it loses. If the electron hasn't reached the wall, the process repeats until it does. Then, the program repeats the whole process again until it has simulated 100,000 electrons. Then, I ran my output through my professor's code, which does a similar thing with the detector design we're using. Altogether, these simulations show what we should expect as an output, should we see some variation in the tritium density, and gives a baseline for the systematic uncertainties we should expect. It also gives us some commentary on the feasibility of the detector design.
I have a point, but you'll have to read on.
At the beginning of baseball season every year, you can usually find some article online talking about computer algorithms that predict the outcomes of the coming season. These algorithms calculate how many games a team will win, how many runs they will score, their likelihood of making the playoffs, and much more. The way they do it is actually quite simple (in principle).
These algorithms merely take the rosters of each team, and uses each players' projected stats to calculate the likelihood of every possible outcome of any particular pitcher-batter match-up. Using these stats, the algorithms simulate every game of the season, one plate appearance at a time. They then repeat the algorithm about a thousand times to minimize uncertainties in random variations.
Hopefully you're starting to see a pattern. Here's another example:
Last fall, I watched a few episodes of a show called "Deadliest Warrior". The premise of the show is that they explore and analyze the weapons and fighting techniques of some of history's most famous warriors, and try to answer the question of who was more lethal. It's the perfect show for any guy who has ever sat around drinking with his buddies and asked the question, "Hey, if a samurai and a viking ever fought to the death, who would win?" The answer, of course- the samurai.
Anyway, so here's how the show went about answering this question: First, they invited experts and martial artists to showcase the weapons and techniques of each side, running tests on each weapon to determine its killing ability. Then, they put the data into a computer program that simulated the battle, blow by blow, a thousand times and tallied the wins for each side.
I'm not an expert in financial markets, but I'm pretty sure they do something similar there as well.
So, maybe my point is this: The work that goes on in the Physics world doesn't need to seem so distant and scary. There are many people out there who do very similar work in fields that are much more accessible to the general public.
As a matter of fact, my job is much easier than those that I highlighted earlier. My program is about 100 lines of Python code. Sports and battle simulations are much harder to do.
For example, those computer algorithms seem to predict the Yankees winning the world series every year. This year is the first since 2000 that they've been right.
...And I think we know what kind of track record the banking industry has...
Sunday, July 19, 2009
Heisenberg Uncertainty
One of the things that just about everyone knows about quantum mechanics is that it is a theory that only predicts probabilities. In other words, even if you know everything about a particle there is to know, you still may not be able to say where it is. The only thing quantum mechanics can tell you is the probability of detecting the particle in any given location. This fact does not have a famous name, but is often referred to as the indeterminacy of quantum mechanics. What it is not called, however, is the Heisenberg uncertainty principle. I've heard everyone from John Stewart to cult-recruitment movies get this little bit of terminology wrong. This post is about what the Heisenberg uncertainty principle actually is.
The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.
The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.
Wednesday, July 8, 2009
Quantum Mechanics
Quantum Mechanics is one of the most popular yet misunderstood physics topics out there. There are many myths around quantum mechanics that I run into from time to time, and I thought I'd devote some posts to the topic.
Perhaps the biggest myth surrounding quantum mechanics is the idea that it doesn't make sense. This idea is absurd. Quantum mechanics describes how our world works- if it doesn't make sense, then you just don't understand it. Or at least you haven't thought about it in the right way.
Quantum mechanics is baffling yet incredibly simple. You can literally write down all of quantum mechanics on a half-sheet of paper. As a matter of fact, here it is:
- The state of a system is entirely represented by its wave function, which is a unit vector of any number of dimensions (including infinite) existing in Hilbert space. The wave function can be calculated from the Schrodinger equation:
- The expectation value (in a statistical sense) of an observable quantity is the inner product of the wave function with the wave function after being operated on by the observable's hermitian operator.
- Determinate States, or states of a system that correspond to a constant observed value, are eigenstates of the observable's hermitian operator, while the observed value is the eigenvalue. (ex. energy levels that give rise to discrete atomic spectra are eigenvalues corresponding to energy determinate states.)
- All determinate states are orthogonal and all possible states can be expressed as a linear combination of determinate states.
- When a measurement is made, the probability of getting a certain value is the square root of the inner product of that value's determinate state with the wave function.
- Upon measurement, the wave function "collapses", becoming the determinate state corresponding to the value that was measured.
So how bad was that?
Okay, so this is probably confusing to those of you who haven't had a class in quantum mechanics or an advanced course in linear algebra. Getting passed the math, it really isn't that hard conceptually. The important thing to note, though, is the fact that it can be defined so concisely. I think I've actually included more than necessary, so it probably can be even more concise than what I've written. Quantum mechanics is pretty complex in application, but is simple at its core. All of the best theories have this quality.
I'll probably post some stuff later that will (hopefully) clear up some of the details.
Another myth I run into is around the term "Quantum Physicist". There isn't such thing- at least in the professional sense. The reason why is the fact that there isn't a physicist in the world who doesn't use quantum mechanics. If the term "Quantum Physicist" represents a scientist who uses quantum mechanics in his/her research, we can probably just agree to just use the term "Physicist". Likewise, it is impossible to go to college and major in "Quantum Physics". Any respectable university would require its physics majors to learn quantum mechanics, so there is no reason to create a new major around it. I'm saying this in reference to the nerdy characters in movies and TV shows who are described using these terms. If you know anyone who writes screenplays, let them know.
I was going to get into some of the misunderstandings around actual quantum mechanics, but maybe I'll get into it later. Most of these misunderstandings involve the indeterminacy of the statistical interpretation, the Heisenberg uncertainty principle, and the collapse of the wave function. I'll try to get to all these issues later. For now, I'm hungry.
Perhaps the biggest myth surrounding quantum mechanics is the idea that it doesn't make sense. This idea is absurd. Quantum mechanics describes how our world works- if it doesn't make sense, then you just don't understand it. Or at least you haven't thought about it in the right way.
Quantum mechanics is baffling yet incredibly simple. You can literally write down all of quantum mechanics on a half-sheet of paper. As a matter of fact, here it is:
- The state of a system is entirely represented by its wave function, which is a unit vector of any number of dimensions (including infinite) existing in Hilbert space. The wave function can be calculated from the Schrodinger equation:
- The expectation value (in a statistical sense) of an observable quantity is the inner product of the wave function with the wave function after being operated on by the observable's hermitian operator.
- Determinate States, or states of a system that correspond to a constant observed value, are eigenstates of the observable's hermitian operator, while the observed value is the eigenvalue. (ex. energy levels that give rise to discrete atomic spectra are eigenvalues corresponding to energy determinate states.)
- All determinate states are orthogonal and all possible states can be expressed as a linear combination of determinate states.
- When a measurement is made, the probability of getting a certain value is the square root of the inner product of that value's determinate state with the wave function.
- Upon measurement, the wave function "collapses", becoming the determinate state corresponding to the value that was measured.
So how bad was that?
Okay, so this is probably confusing to those of you who haven't had a class in quantum mechanics or an advanced course in linear algebra. Getting passed the math, it really isn't that hard conceptually. The important thing to note, though, is the fact that it can be defined so concisely. I think I've actually included more than necessary, so it probably can be even more concise than what I've written. Quantum mechanics is pretty complex in application, but is simple at its core. All of the best theories have this quality.
I'll probably post some stuff later that will (hopefully) clear up some of the details.
Another myth I run into is around the term "Quantum Physicist". There isn't such thing- at least in the professional sense. The reason why is the fact that there isn't a physicist in the world who doesn't use quantum mechanics. If the term "Quantum Physicist" represents a scientist who uses quantum mechanics in his/her research, we can probably just agree to just use the term "Physicist". Likewise, it is impossible to go to college and major in "Quantum Physics". Any respectable university would require its physics majors to learn quantum mechanics, so there is no reason to create a new major around it. I'm saying this in reference to the nerdy characters in movies and TV shows who are described using these terms. If you know anyone who writes screenplays, let them know.
I was going to get into some of the misunderstandings around actual quantum mechanics, but maybe I'll get into it later. Most of these misunderstandings involve the indeterminacy of the statistical interpretation, the Heisenberg uncertainty principle, and the collapse of the wave function. I'll try to get to all these issues later. For now, I'm hungry.
Wednesday, April 15, 2009
Why I (Really) Like Physics (part III)
Energy is a physics concept that has been around forever. Energy conservation is firmly ingrained in the minds of theorists as the one law which has and will never be broken. This simple concept, however, leads to some pretty cool things to think about if you have the time.
Energy is one of those things you learned about if you took a high school or college physics course. You probably learned about it and found that it made many problems easier to solve, but didn't think much of it. Here's a summary of what your physics teacher mentioned:
When you make an object move by imparting a force onto it, you exert work while the object gains energy. We define the amount of energy the object has as the amount of work you had to exert to get it into the state it is in. For example, if you push a cart down the street, it begins to move and attains velocity. The motion of the cart is a form of energy called kinetic energy.
Another example- When you lift up a bowling ball, you are exerting a force on the ball to counteract the force of gravity. The energy gained by the ball is called gravitational potential energy. It is called 'potential' energy because it has the potential to become something else.
For example, if you were to drop that bowling ball, the ball's gravitational potential energy would be converted into kinetic energy, and it suddenly becomes very simple to calculate how fast the ball is traveling the instant before it hits you in the foot.
What we call "conservation of energy" is the thing that makes the concept of energy so useful. The really cool thing about it, however, is that the whole concept of energy really just came about as a mathematical trick- a mathematical trick that turned out to reveal something incredibly profound (another such example would be of entropy, which was used in thermodynamics as a math trick long before people realized it actually represented a physical quantity). Here's a little bit of background in classical mechanics:
In Newtonian mechanics, everything is derived from four assumptions: Newton's three laws of motion, and Newton's law of gravity. The three laws state that: (1) an object in motion stays in motion unless acted upon by a force, (2) force equals mass times acceleration, and (3) when one object exerts a force on another, the second object exerts an equal force on the first in the opposite direction. Newton's law of gravity just establishes the nature of gravitational forces between two massive objects. These four assumptions are a physicist's dream. They are simple and concise, yet describe a huge mess of observations- including Kepler's laws, which had previously gone unexplained for decades.
So, where in these assumptions does energy come in? The answer is it doesn't- at least not explicitly. There's a whole lot of talk about forces, but nothing about energy. Nothing that is, until someone comes along and shows that you can prove (from Newton's laws) that the total energy in a closed system is always constant (that is, so long as there's no friction). In Newtonian mechanics, the concept of energy is purely optional. In principle, you could use Newton's laws to solve for anything you'd like to without the word 'energy' so much as crossing your mind.
Now, lets return to the bowling ball example we went through before. You may have noticed that I intentionally only took the example through to the point right before the bowling ball lands. So let's ask the obvious question now- What happens to the bowling ball's energy after it lands? I think we're in agreement that the bowling ball stops after landing, so its kinetic energy is gone, and it no longer has the potential energy it has before you drop it. Conservation of energy isn't very useful if chunks of energy can suddenly disappear without explanation.
Well, that question was answered by James Joule, a physicist whose work is so essential that the standard unit of energy is named after him. What Joule did that was so important is he forced water through a perforated tube and observed that the temperature of the water increased. He also did a similar experiment by heating water with an electrical energy source. The conclusion that was reached from these experiments was the fact that heat, which was understood to be a substance that made the temperature of objects rise, was really just another form of energy.
So, the answer to our bowling ball crashing to the floor question is this: The bowling ball heats up the floor. Some of the energy also escapes in the form of sound waves, which eventually dissipate by heating up the walls and other objects they bump into. The important thing to notice is the fact that conservation of energy, which was originally our little mathematical trick, is still true in the face of forces that we didn't really consider in the first place.
These forces I'm referring to are called non-conservative forces and include things like friction and wind resistance. The thing that these forces share is that they all create heat. The reason they're called non-conservative is the fact that once energy is converted into heat, it becomes theoretically impossible to convert all of it back into some other form (this is where entropy comes in). This isn't to say that the energy is not conserved- it is only converted to a form that makes it irretrievable.
Now that we've cleared that up, lets look at the bowling ball example from the other way: Where did the energy that raised the bowling ball come from?
Well, the energy that powers your muscles is released in a chemical reaction that converts ATP into ADP. The energy that was used to create the ATP in the first place comes from chemical reactions that convert the food you eat into waste product. The energy stored in food, if you trace it back, originates from photons that travel from the sun and are absorbed in the leaves of plants. I'm sure you all are familiar with the Calorie and all of its stress-inducing properties. But did you know that the Calorie is really just another unit of energy? You could literally take the caloric content of a jelly donut and calculate how many bowling balls you could lift with the energy it provides.
Now, speaking of photons from the sun- the sun gets its energy from the fusion reaction in its core which continuously converts hydrogen into helium, releasing a lot of energy. This reaction has the effect of heating up the star to high temperatures and photons are emitted through blackbody radiation. Just about all sources of energy we use today originate from this blackbody radiation. The exception comes in if you happen to live in an area which is powered by a nuclear reactor. The energy in that case comes from a nuclear reaction involving radioactive isotopes you can find in the soil of your lawn (albeit in tiny quantities).
If you're being really thorough, you might remind yourself that all the energy that powers the sun, as well as your neighborhood nuclear reactor, was released to the universe in the big bang.
To this day, conservation of energy remains one of the few conservation laws that has not been violated, even in the face of other vast changes to physical law. Take, for example, Einstein's relativity. Changes were made to our understanding of energy that you'd never see coming. Formulas like those for kinetic energy had to be completely changed (the speed of light started showing up everywhere!). It turned out that mass was really another form of energy. Despite these changes (or because of them), the basic tenant that the energy of a system is constant remained intact. So many ideas that were firmly ingrained in our minds regarding things like mass, time, and space were thrown away while energy was one of the few that remained.
So, here's another example of something more modern that would seem very strange in Newton's days. A piece of gamma radiation (which is really just a high-energy photon), if it has enough energy, can interact with a nuclear electric field, disappear, and create an electron-positron pair. The electron goes off and does what an electron does, but the positron, which is basically a positively-charged electron, does something that is truly remarkable. The positron bounces around until it loses its kinetic energy, eventually getting trapped in the electric field of an electron. The two particles then annihilate each other, and in their place two gamma rays are emitted in opposite directions.
Care to guess what the energies of these two gamma rays are? Well, if you recall Einstein's mass-energy relation, E = mc^2, you can calculate the rest energy of both the positron and electron, and it happens to be 511 KeV. The energy of the two gamma rays are, not coincidentally, also 511 KeV. The two gamma rays carry off the energy that was released when the electron and positron disappeared.
The example above illustrates what the world of modern particle physics is like. Particles routinely appear and disappear and do other things you wouldn't imagine is possible. Imagine for a second what the world would be like if two baseballs could collide and both subsequently disappear in a huge flash of light. The laws that govern the things we normally see on a daily basis don't apply at the particle level, yet things still follow the basic tenant of conservation of energy, which we knew from Newton's days and didn't need to exist in the first place. Things didn't need to be that way.
As remarkable as the concept of energy is, one might find that it is also a necessary one. After all, the universe would not have any semblance of order unless there was something that was held constant. That 'something' was something we just happened to call "energy".
Energy is one of those things you learned about if you took a high school or college physics course. You probably learned about it and found that it made many problems easier to solve, but didn't think much of it. Here's a summary of what your physics teacher mentioned:
When you make an object move by imparting a force onto it, you exert work while the object gains energy. We define the amount of energy the object has as the amount of work you had to exert to get it into the state it is in. For example, if you push a cart down the street, it begins to move and attains velocity. The motion of the cart is a form of energy called kinetic energy.
Another example- When you lift up a bowling ball, you are exerting a force on the ball to counteract the force of gravity. The energy gained by the ball is called gravitational potential energy. It is called 'potential' energy because it has the potential to become something else.
For example, if you were to drop that bowling ball, the ball's gravitational potential energy would be converted into kinetic energy, and it suddenly becomes very simple to calculate how fast the ball is traveling the instant before it hits you in the foot.
What we call "conservation of energy" is the thing that makes the concept of energy so useful. The really cool thing about it, however, is that the whole concept of energy really just came about as a mathematical trick- a mathematical trick that turned out to reveal something incredibly profound (another such example would be of entropy, which was used in thermodynamics as a math trick long before people realized it actually represented a physical quantity). Here's a little bit of background in classical mechanics:
In Newtonian mechanics, everything is derived from four assumptions: Newton's three laws of motion, and Newton's law of gravity. The three laws state that: (1) an object in motion stays in motion unless acted upon by a force, (2) force equals mass times acceleration, and (3) when one object exerts a force on another, the second object exerts an equal force on the first in the opposite direction. Newton's law of gravity just establishes the nature of gravitational forces between two massive objects. These four assumptions are a physicist's dream. They are simple and concise, yet describe a huge mess of observations- including Kepler's laws, which had previously gone unexplained for decades.
So, where in these assumptions does energy come in? The answer is it doesn't- at least not explicitly. There's a whole lot of talk about forces, but nothing about energy. Nothing that is, until someone comes along and shows that you can prove (from Newton's laws) that the total energy in a closed system is always constant (that is, so long as there's no friction). In Newtonian mechanics, the concept of energy is purely optional. In principle, you could use Newton's laws to solve for anything you'd like to without the word 'energy' so much as crossing your mind.
Now, lets return to the bowling ball example we went through before. You may have noticed that I intentionally only took the example through to the point right before the bowling ball lands. So let's ask the obvious question now- What happens to the bowling ball's energy after it lands? I think we're in agreement that the bowling ball stops after landing, so its kinetic energy is gone, and it no longer has the potential energy it has before you drop it. Conservation of energy isn't very useful if chunks of energy can suddenly disappear without explanation.
Well, that question was answered by James Joule, a physicist whose work is so essential that the standard unit of energy is named after him. What Joule did that was so important is he forced water through a perforated tube and observed that the temperature of the water increased. He also did a similar experiment by heating water with an electrical energy source. The conclusion that was reached from these experiments was the fact that heat, which was understood to be a substance that made the temperature of objects rise, was really just another form of energy.
So, the answer to our bowling ball crashing to the floor question is this: The bowling ball heats up the floor. Some of the energy also escapes in the form of sound waves, which eventually dissipate by heating up the walls and other objects they bump into. The important thing to notice is the fact that conservation of energy, which was originally our little mathematical trick, is still true in the face of forces that we didn't really consider in the first place.
These forces I'm referring to are called non-conservative forces and include things like friction and wind resistance. The thing that these forces share is that they all create heat. The reason they're called non-conservative is the fact that once energy is converted into heat, it becomes theoretically impossible to convert all of it back into some other form (this is where entropy comes in). This isn't to say that the energy is not conserved- it is only converted to a form that makes it irretrievable.
Now that we've cleared that up, lets look at the bowling ball example from the other way: Where did the energy that raised the bowling ball come from?
Well, the energy that powers your muscles is released in a chemical reaction that converts ATP into ADP. The energy that was used to create the ATP in the first place comes from chemical reactions that convert the food you eat into waste product. The energy stored in food, if you trace it back, originates from photons that travel from the sun and are absorbed in the leaves of plants. I'm sure you all are familiar with the Calorie and all of its stress-inducing properties. But did you know that the Calorie is really just another unit of energy? You could literally take the caloric content of a jelly donut and calculate how many bowling balls you could lift with the energy it provides.
Now, speaking of photons from the sun- the sun gets its energy from the fusion reaction in its core which continuously converts hydrogen into helium, releasing a lot of energy. This reaction has the effect of heating up the star to high temperatures and photons are emitted through blackbody radiation. Just about all sources of energy we use today originate from this blackbody radiation. The exception comes in if you happen to live in an area which is powered by a nuclear reactor. The energy in that case comes from a nuclear reaction involving radioactive isotopes you can find in the soil of your lawn (albeit in tiny quantities).
If you're being really thorough, you might remind yourself that all the energy that powers the sun, as well as your neighborhood nuclear reactor, was released to the universe in the big bang.
To this day, conservation of energy remains one of the few conservation laws that has not been violated, even in the face of other vast changes to physical law. Take, for example, Einstein's relativity. Changes were made to our understanding of energy that you'd never see coming. Formulas like those for kinetic energy had to be completely changed (the speed of light started showing up everywhere!). It turned out that mass was really another form of energy. Despite these changes (or because of them), the basic tenant that the energy of a system is constant remained intact. So many ideas that were firmly ingrained in our minds regarding things like mass, time, and space were thrown away while energy was one of the few that remained.
So, here's another example of something more modern that would seem very strange in Newton's days. A piece of gamma radiation (which is really just a high-energy photon), if it has enough energy, can interact with a nuclear electric field, disappear, and create an electron-positron pair. The electron goes off and does what an electron does, but the positron, which is basically a positively-charged electron, does something that is truly remarkable. The positron bounces around until it loses its kinetic energy, eventually getting trapped in the electric field of an electron. The two particles then annihilate each other, and in their place two gamma rays are emitted in opposite directions.
Care to guess what the energies of these two gamma rays are? Well, if you recall Einstein's mass-energy relation, E = mc^2, you can calculate the rest energy of both the positron and electron, and it happens to be 511 KeV. The energy of the two gamma rays are, not coincidentally, also 511 KeV. The two gamma rays carry off the energy that was released when the electron and positron disappeared.
The example above illustrates what the world of modern particle physics is like. Particles routinely appear and disappear and do other things you wouldn't imagine is possible. Imagine for a second what the world would be like if two baseballs could collide and both subsequently disappear in a huge flash of light. The laws that govern the things we normally see on a daily basis don't apply at the particle level, yet things still follow the basic tenant of conservation of energy, which we knew from Newton's days and didn't need to exist in the first place. Things didn't need to be that way.
As remarkable as the concept of energy is, one might find that it is also a necessary one. After all, the universe would not have any semblance of order unless there was something that was held constant. That 'something' was something we just happened to call "energy".
Monday, April 6, 2009
Why I (Actually) Like Physics (part II)
Physics is so friggin' awesome- especially when it gives you an opportunity to go off and play in Santa Barbara for a few years and (hopefully) wait out the recession.
Physics also gives rise to sites like this:
Only physics would give people the opportunity to watch a giant blimp-like object get wheeled through a small town in Germany.
By the way, the blimp-like object in question is a major piece of the KATRIN experiment, which I will probably be a part of come this fall. The purpose of the experiment is to measure the mass of the neutrino.
The neutrino, for those of you who don't know, is an elementary particle that still remains a mystery to physicists in many ways. The fact that we still don't have a clue as to its mass at this point is evidence enough for this claim. The reason we know so little about this particle is that it only interacts via the weak force- or in other words, it hardly interacts with anything. Because a particle has to interact with something before it is detected, this makes the goal of actually detecting these things incredibly hard. There are many experiments today that tackle this immense challenge, but there's something cool about KATRIN that I'd like to mention.
You see, KATRIN will attempt to measure the mass of the neutrino, without actually detecting them!
All the experiment is really going to do is measure the energy spectrum of tritium beta decay electrons. You see, when tritium decays, it produces three products: a Helium-3 nucleus, an electron, and a neutrino. The total energy released in the decay is constant and known, and must be distributed among the three products. As we know from Einstein's mass-energy equivalence, part of this energy must be spent in the creation of the neutrino itself, which makes the distribution of electron energies dependent upon the neutrino's mass.
Of course, the experiment itself isn't THAT simple. Obtaining an energy resolution good enough for the mass range we're probing is no small task, and there is a lot of work being done to make sure all the little things are taken care of.
There's also the possibility that the experiment will produce nothing at all...
But all in all, you must agree that the whole picture is nothing but pure awesome.
Physics also gives rise to sites like this:
Only physics would give people the opportunity to watch a giant blimp-like object get wheeled through a small town in Germany.
By the way, the blimp-like object in question is a major piece of the KATRIN experiment, which I will probably be a part of come this fall. The purpose of the experiment is to measure the mass of the neutrino.
The neutrino, for those of you who don't know, is an elementary particle that still remains a mystery to physicists in many ways. The fact that we still don't have a clue as to its mass at this point is evidence enough for this claim. The reason we know so little about this particle is that it only interacts via the weak force- or in other words, it hardly interacts with anything. Because a particle has to interact with something before it is detected, this makes the goal of actually detecting these things incredibly hard. There are many experiments today that tackle this immense challenge, but there's something cool about KATRIN that I'd like to mention.
You see, KATRIN will attempt to measure the mass of the neutrino, without actually detecting them!
All the experiment is really going to do is measure the energy spectrum of tritium beta decay electrons. You see, when tritium decays, it produces three products: a Helium-3 nucleus, an electron, and a neutrino. The total energy released in the decay is constant and known, and must be distributed among the three products. As we know from Einstein's mass-energy equivalence, part of this energy must be spent in the creation of the neutrino itself, which makes the distribution of electron energies dependent upon the neutrino's mass.
Of course, the experiment itself isn't THAT simple. Obtaining an energy resolution good enough for the mass range we're probing is no small task, and there is a lot of work being done to make sure all the little things are taken care of.
There's also the possibility that the experiment will produce nothing at all...
But all in all, you must agree that the whole picture is nothing but pure awesome.
Tuesday, March 10, 2009
I'm a geek
Yes, I am a geek. I'm sure you all knew this fact- especially if you've read some of my earlier posts. I'm aware that the fact that I study physics (and enjoy it) is enough to include me in that category.
Let me share with you the moment that I realized that I was a true geek. I suppose I knew it long before, but this is the first time that the fact really hit home.
The moment came when I was watching the movie Spiderman II. If you're familiar with the story, you know that Spiderman's alter ego, Peter Parker, is also a geek. Now you see, in a movie it's not enough to tell the viewers that Spiderman is a nerd, you have to show it. And what better way to show that the story's superhero is just a supernerd is there than to show him in a lecture hall, completely infatuated with the strange symbols written on the board by an old balding nerd of a professor.
If you saw the movie, this short scene probably made you think, "wow, that guy is a geek!" However, the thought that popped into MY head was, "Hey! We just covered that material last week in Quantum Mechanics!"
Wow! I'm just as nerdy as Spiderman!!!
Now all I need is a radioactive spider....
Of course, not all depictions of geeks in motion pictures are quite as flattering as Spiderman. I must say, however, that I still enjoy watching them- but not for the reasons you might enjoy them.
Let me give another example to illustrate. This one comes from the movie Transformers. I've never actually seen the movie, but a friend told me about this scene and it had me practically rolling on the floor with laughter. The scene goes something like this:
Two nerdy scientists are in a lab, and one turns to the other and says, in a British accent: "Why don't you STOP thinking about Fourier transforms and START thinking about Quantum Mechanics?!"
Now, you might not think that this sentence is particularly funny, but my friend and I both did, and for the same reason. You see, whoever wrote this stupid dialogue obviously has no idea what the terms 'Fourier transform' and 'Quantum Mechanics' even mean. If you are intimately familiar with these two terms, you would know that no scientist sitting in a lab would ever utter that sentence.
This sort of dialogue is the kind that I hear all the time in movies and on tv. It's the kind of dialogue that just screams, "this is the smartest sounding sentence that the writer could come up with".
It just goes to show that while you're making fun of nerds for their lack of athletic ability and social grace, they're probably making fun of you for being an idiot.
Let me share with you the moment that I realized that I was a true geek. I suppose I knew it long before, but this is the first time that the fact really hit home.
The moment came when I was watching the movie Spiderman II. If you're familiar with the story, you know that Spiderman's alter ego, Peter Parker, is also a geek. Now you see, in a movie it's not enough to tell the viewers that Spiderman is a nerd, you have to show it. And what better way to show that the story's superhero is just a supernerd is there than to show him in a lecture hall, completely infatuated with the strange symbols written on the board by an old balding nerd of a professor.
If you saw the movie, this short scene probably made you think, "wow, that guy is a geek!" However, the thought that popped into MY head was, "Hey! We just covered that material last week in Quantum Mechanics!"
Wow! I'm just as nerdy as Spiderman!!!
Now all I need is a radioactive spider....
Of course, not all depictions of geeks in motion pictures are quite as flattering as Spiderman. I must say, however, that I still enjoy watching them- but not for the reasons you might enjoy them.
Let me give another example to illustrate. This one comes from the movie Transformers. I've never actually seen the movie, but a friend told me about this scene and it had me practically rolling on the floor with laughter. The scene goes something like this:
Two nerdy scientists are in a lab, and one turns to the other and says, in a British accent: "Why don't you STOP thinking about Fourier transforms and START thinking about Quantum Mechanics?!"
Now, you might not think that this sentence is particularly funny, but my friend and I both did, and for the same reason. You see, whoever wrote this stupid dialogue obviously has no idea what the terms 'Fourier transform' and 'Quantum Mechanics' even mean. If you are intimately familiar with these two terms, you would know that no scientist sitting in a lab would ever utter that sentence.
This sort of dialogue is the kind that I hear all the time in movies and on tv. It's the kind of dialogue that just screams, "this is the smartest sounding sentence that the writer could come up with".
It just goes to show that while you're making fun of nerds for their lack of athletic ability and social grace, they're probably making fun of you for being an idiot.
Sunday, March 8, 2009
"Political Economics"
There is something in the study of economics that's been bothering me for a bit. Now, I don't claim to really know ANYTHING when it comes to economics, nor have I stepped foot in an economics class or opened an economics textbook since high school. Nevertheless, the subject of today's economy has been too pervasive in the media to ignore, and I've been bothered by a few things I've found troubling- not relating to the economy itself, but by how people deal with it.
Now, let me explain something I've learned about physics research. Physicists always know what to expect from an experiment. That isn't to say that they always know the outcome, since that would make the experiment useless. Physicists use the accepted laws of physics to predict the outcome, and when the outcome does not agree with the laws, they know that something is wrong with the theory. Predicting outcomes is no easy task in today's large-scale experiments, but the standards are just as high. Doing so usually requires the use of sophisticated modeling algorithms and lots of computing power.
Let me give you an example: One professor I talked to at Berkeley gave me a sneak peak at some of the software that was developed for one of the projects in development at the LHC called ATLAS. The ATLAS detector is about the size of a mansion, and the laws that govern the interactions between particles are in no way simple. Nevertheless, software that incorporates all these parameters have been developed since long before the actual detector began construction. Through the computer simulations given from this program, my professor was able to show me exactly what we would see from the detectors, with charts, graphs, and everything you might expect from a large scale experiment. She even showed me the bump on a particular graph that would prove the existence of the Higgs boson. These graphs and charts were made a long time ago, and yet to this day they haven't even started colliding particles at the LHC.
No matter how much a certain experiment costs- from a few thousand to several billion- researchers are held to the same rigorous standards. They must show exactly why the experiment will work, and exactly what the experiment will establish (or no funding!).
Now, to see why I'm a little peeved, let me ask this question: What did Obama do to show that his $3/4 trillion stimulus package would work? All I've heard is a few political sound bites- from both sides of the aisle.
I'm not saying I'm against the package. I'd say I'm cautiously optimistic about it (I voted for Obama, after all). I, however, am concerned with the fact that I've never seen a shred of evidence relating to economic policies. I've heard arguments, but evidence is apparently hard to come by.
I'm aware that economics are quite a bit different from physics. It's definitely harder (maybe impossible) to simulate an economy inside a computer; the variables are uncountable, and people as a whole are unpredictable- even in a statistical sense (that's probably what separates us from animals).
However, economics is a real area of study. People get PhDs in the subject. Papers are published on a regular basis. A Nobel Prize is awarded in economics EVERY YEAR for crying out loud!!! I can't imagine that there isn't a shred of evidence out there that supports the conclusions they make. Why don't they let us see it?
The reason why, I think, is that the people who talk to us about the economy aren't economists- They're politicians. The burden of proof no longer exists when good salesmanship will achieve the same end.
This, coincidentaly, is the other thing I don't like about economics: It's impossible to separate it from the politics that drive it. I can't help but draw a parallel between today's economic theories and the phrase "Christian science". No scientific theory is viable if it is influenced by ideas taken from religious beliefs. In the same way, I won't believe in an economic theory if its purpose is to back up someone's politics.
In other words, I won't believe anyone when they say that tax cuts are the key to fixing the economy. It could be true, but I can't shake the feeling that the theory behind it was just drummed up to get a few more votes. I'm sure there are a lot of smart people with PhDs that can show me exactly why tax cuts will fix the economy, but then again, there are probably smart people with PhDs that will show me exactly why they won't.
And here's another thing: If Nobel prizes are awarded in economics every year, why is it that I haven't heard any new economic ideas in the last decade? I'd use a longer time frame, but I don't think I was politically aware enough more than ten years ago to formulate a comparison.
Maybe my views on economics are merely a result of my ignorance. I'm sure there are those who can prove all of the statements in this post wrong, but you know what? I'd rather hear it from Washington. Then maybe I'd think that those losers actually know something.
Now, let me explain something I've learned about physics research. Physicists always know what to expect from an experiment. That isn't to say that they always know the outcome, since that would make the experiment useless. Physicists use the accepted laws of physics to predict the outcome, and when the outcome does not agree with the laws, they know that something is wrong with the theory. Predicting outcomes is no easy task in today's large-scale experiments, but the standards are just as high. Doing so usually requires the use of sophisticated modeling algorithms and lots of computing power.
Let me give you an example: One professor I talked to at Berkeley gave me a sneak peak at some of the software that was developed for one of the projects in development at the LHC called ATLAS. The ATLAS detector is about the size of a mansion, and the laws that govern the interactions between particles are in no way simple. Nevertheless, software that incorporates all these parameters have been developed since long before the actual detector began construction. Through the computer simulations given from this program, my professor was able to show me exactly what we would see from the detectors, with charts, graphs, and everything you might expect from a large scale experiment. She even showed me the bump on a particular graph that would prove the existence of the Higgs boson. These graphs and charts were made a long time ago, and yet to this day they haven't even started colliding particles at the LHC.
No matter how much a certain experiment costs- from a few thousand to several billion- researchers are held to the same rigorous standards. They must show exactly why the experiment will work, and exactly what the experiment will establish (or no funding!).
Now, to see why I'm a little peeved, let me ask this question: What did Obama do to show that his $3/4 trillion stimulus package would work? All I've heard is a few political sound bites- from both sides of the aisle.
I'm not saying I'm against the package. I'd say I'm cautiously optimistic about it (I voted for Obama, after all). I, however, am concerned with the fact that I've never seen a shred of evidence relating to economic policies. I've heard arguments, but evidence is apparently hard to come by.
I'm aware that economics are quite a bit different from physics. It's definitely harder (maybe impossible) to simulate an economy inside a computer; the variables are uncountable, and people as a whole are unpredictable- even in a statistical sense (that's probably what separates us from animals).
However, economics is a real area of study. People get PhDs in the subject. Papers are published on a regular basis. A Nobel Prize is awarded in economics EVERY YEAR for crying out loud!!! I can't imagine that there isn't a shred of evidence out there that supports the conclusions they make. Why don't they let us see it?
The reason why, I think, is that the people who talk to us about the economy aren't economists- They're politicians. The burden of proof no longer exists when good salesmanship will achieve the same end.
This, coincidentaly, is the other thing I don't like about economics: It's impossible to separate it from the politics that drive it. I can't help but draw a parallel between today's economic theories and the phrase "Christian science". No scientific theory is viable if it is influenced by ideas taken from religious beliefs. In the same way, I won't believe in an economic theory if its purpose is to back up someone's politics.
In other words, I won't believe anyone when they say that tax cuts are the key to fixing the economy. It could be true, but I can't shake the feeling that the theory behind it was just drummed up to get a few more votes. I'm sure there are a lot of smart people with PhDs that can show me exactly why tax cuts will fix the economy, but then again, there are probably smart people with PhDs that will show me exactly why they won't.
And here's another thing: If Nobel prizes are awarded in economics every year, why is it that I haven't heard any new economic ideas in the last decade? I'd use a longer time frame, but I don't think I was politically aware enough more than ten years ago to formulate a comparison.
Maybe my views on economics are merely a result of my ignorance. I'm sure there are those who can prove all of the statements in this post wrong, but you know what? I'd rather hear it from Washington. Then maybe I'd think that those losers actually know something.
Tuesday, February 17, 2009
Why I (actually) like physics (part I)
I'm not sure how many parts there will be, but I don't think this post will say everything I'd like to. To follow is just one example that I hope illustrates what it is I like about physics.
I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:
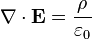
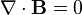
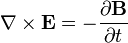

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...
I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:
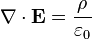
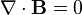
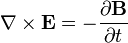

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...
Monday, February 9, 2009
What I don't like about physics
One of the first things my wife ever asked me was the question, "Why do you like physics?" I don't think I ever answered that question for her- or at least not directly. After all, I don't think I really had a good answer back then.
The reason I chose to study physics was pretty simple: I felt that I was good at it. I chose to study physics while taking an advanced placement physics course in high school with my older brother. The classroom was filled with some of the smartest kids in school, many of whom were struggling pathetically- asking stupid questions with obviously no clue as to how to do any of the problems. I don't mean to brag, but I slept through class every other day and aced pretty much every test. Yes, I suppose I must be a genius, and that's just me being modest.
But, the question my wife asked was "Why do you like physics?", which requires a different answer entirely. I think I have a much better idea today than I did way back then, but it is still a question that I am hesitant to answer.
After all, when was the last time you heard someone say the phrase "I love physics" without having to wonder how long it has been since he last brushed his teeth?....or at least wonder how many hours he spends leveling up his elven rogue. I also feel that people who talk about physics a lot do so under the impression that people are impressed by it. Take the following conversation:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........You must be really smart!"
Yeah, so you may think that the person in the conversation above is impressed with my intellectual mastery, but if you could see the facial expressions that accompany the dialogue, you would probably have a different idea. Lets revisit the above conversation, but instead here's what the people involved are actually thinking:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........Why would you do that to yourself?"
"I suppose our conversation is over, huh?"
"Yeah.....So what level is your elven rogue?"
In college I learned to hate that conversation. Nevertheless, I'm still going to try to answer that question that my wife asked so long ago. Just keep in mind that physicists can still be cool. Richard Feynman is proof.
I've been typing for a while, and its late so maybe I'll do it later.
The reason I chose to study physics was pretty simple: I felt that I was good at it. I chose to study physics while taking an advanced placement physics course in high school with my older brother. The classroom was filled with some of the smartest kids in school, many of whom were struggling pathetically- asking stupid questions with obviously no clue as to how to do any of the problems. I don't mean to brag, but I slept through class every other day and aced pretty much every test. Yes, I suppose I must be a genius, and that's just me being modest.
But, the question my wife asked was "Why do you like physics?", which requires a different answer entirely. I think I have a much better idea today than I did way back then, but it is still a question that I am hesitant to answer.
After all, when was the last time you heard someone say the phrase "I love physics" without having to wonder how long it has been since he last brushed his teeth?....or at least wonder how many hours he spends leveling up his elven rogue. I also feel that people who talk about physics a lot do so under the impression that people are impressed by it. Take the following conversation:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........You must be really smart!"
Yeah, so you may think that the person in the conversation above is impressed with my intellectual mastery, but if you could see the facial expressions that accompany the dialogue, you would probably have a different idea. Lets revisit the above conversation, but instead here's what the people involved are actually thinking:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........Why would you do that to yourself?"
"I suppose our conversation is over, huh?"
"Yeah.....So what level is your elven rogue?"
In college I learned to hate that conversation. Nevertheless, I'm still going to try to answer that question that my wife asked so long ago. Just keep in mind that physicists can still be cool. Richard Feynman is proof.
I've been typing for a while, and its late so maybe I'll do it later.
Subscribe to:
Posts (Atom)