I'm currently working as a math tutor. I can't say I'm the best at what I'm doing, but I think I have one thing to brag about to others who have tutored in the past.
You see, there are some people who can teach a kindergartener how to add and subtract. Other people are good at teaching higher maths like calculus to high schoolers.
I, on the other hand, have done both......AT THE SAME TIME!!
Imagine this: I'm sitting at a table in collared shirt and tie. Across from me to the left is just about the cutest 5-year old girl you've ever seen, working on addition and subtraction problems I made up for her. To the right is an 11th grader doing calculus problems. Here's a sample interaction:
".....so, if there are three frogs on a log and two more hop on, NOW how many do you have?"
".....five?"
"GOOD!!!! Now, can you work on these next few problems?"
"...ok....."
(turn)
"Alright, so.....To do this integral, it's probably easiest to use this substitution....."
The place where I work likes to do individualized tutoring, but keeps the cost down by having up to three students per tutor at a time. Tutors are supposed to keep the kids busy by assigning problems during the class period and dividing up the one-on-one time. As you can imagine, it's not usually that simple.
One thing I found strange is that they specifically asked whether I was more comfortable teaching math or verbal, but never asked about what age groups I was comfortable with.
Well, I suppose they did ask me if I could teach kids, but it was after they hired me, and besides, what was I supposed to say?
...Not that I'm bad with kids or anything.
Saturday, February 21, 2009
Wednesday, February 18, 2009
Story
Here's a story.
Once upon a time, there was an 'organization'. This 'organization' was doing very 'well'. 'Investors' of the organization were happy. The organization was making 'lots' of 'money'.
There came a time, however, when 'members' of the organization started 'implementing' 'practices' that would one day threaten the organization. For a time, these 'practices' made the organization do even better. 'Investors' were happy. The organization was making 'lots' of 'money'.
There were several people, other 'members' of the organization, who became aware of these 'practices'. These people took it upon themselves to warn the 'higher-ups' in the organization of these adverse 'practices'. These 'practices', they said, would one day threaten the organization. 'Investors' would be angry. The senate would have hearings. 60 Minutes would do stories.
But the 'higher-ups' of the organization said that there is nothing wrong. After all, the organization is doing 'well'. 'Investors' are happy. The organization is making 'lots' of 'money'.
But there came a time when the 'practices' did, indeed come to threaten the organization. 'Investors' got angry. The senate had hearings. 60 Minutes did stories.
And everyone wondered why the 'higher-ups' did not heed the warnings they had been given. The 'higher-ups' claimed that they were not at fault. They had no reason to do anything about the 'practices' that eventually threatened the organization. After all, at the time, the organization was doing 'well'. 'Investors' were happy, and they were making 'lots' of 'money'.
THE END
So, my astute readers- what is the story about?
The mortgage crisis....
or Major League Baseball?
Once upon a time, there was an 'organization'. This 'organization' was doing very 'well'. 'Investors' of the organization were happy. The organization was making 'lots' of 'money'.
There came a time, however, when 'members' of the organization started 'implementing' 'practices' that would one day threaten the organization. For a time, these 'practices' made the organization do even better. 'Investors' were happy. The organization was making 'lots' of 'money'.
There were several people, other 'members' of the organization, who became aware of these 'practices'. These people took it upon themselves to warn the 'higher-ups' in the organization of these adverse 'practices'. These 'practices', they said, would one day threaten the organization. 'Investors' would be angry. The senate would have hearings. 60 Minutes would do stories.
But the 'higher-ups' of the organization said that there is nothing wrong. After all, the organization is doing 'well'. 'Investors' are happy. The organization is making 'lots' of 'money'.
But there came a time when the 'practices' did, indeed come to threaten the organization. 'Investors' got angry. The senate had hearings. 60 Minutes did stories.
And everyone wondered why the 'higher-ups' did not heed the warnings they had been given. The 'higher-ups' claimed that they were not at fault. They had no reason to do anything about the 'practices' that eventually threatened the organization. After all, at the time, the organization was doing 'well'. 'Investors' were happy, and they were making 'lots' of 'money'.
THE END
So, my astute readers- what is the story about?
The mortgage crisis....
or Major League Baseball?
Tuesday, February 17, 2009
Why I (actually) like physics (part I)
I'm not sure how many parts there will be, but I don't think this post will say everything I'd like to. To follow is just one example that I hope illustrates what it is I like about physics.
I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:
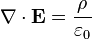
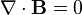
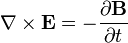

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...
I had a professor at Berkeley- a lanky, bald, British guy who gave very good lectures. This professor, like most professors, liked to enclose the important results and equations in big boxes on the blackboard to let us know that they were important. Every once in a while, we would stumble upon a result so important that they were enclosed in two boxes. Finally, there were three things, (and only three things), that were SO important that they required the use of THREE boxes. These three things were 1. Newton's laws, 2. Maxwell's equations, and 3. The Schrodinger equation. What I'd like to talk about right now is Maxwell's equations. I know what you're thinking, but just stick with me. It should be interesting.......I hope.
While at Berkeley, I was required to take two semesters worth of upper division electricity and magnetism. In the first semester, we took about two weeks to derive Maxwell's equations, and then the rest of the semester, as well as the entire second semester was spent exploring what the equations tell us. So how can a few equations provide a year's worth of material? Maybe we should look at the equations first:
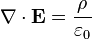
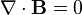
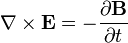

E represents the electric field, while B represents the magnetic. ρ is electric charge, and J is electric current. The other curly Greek letters are constants. Don't worry if you don't know what's going on. Unless you've taken a course in vector calculus, I'm pretty sure you won't.
Overall, the equations are merely statements that show the divergence and curl of the electric and magnetic fields. It has been mathematically proven that knowing the divergence and curl is of a vector field is enough to be able to calculate anything you need to know about the field. In other words, Maxwell's equations tell you EVERYTHING!!!
Here's a breakdown of the equations, one by one:
1. The first equation, Gauss's Law, is probably the least interesting. It is mathematically equivalent to Coulomb's law, which describes the forces between two electric charges. The early experiments that established this law usually involved rubbing glass rods or other objects with cat's fur to create static charge and measuring the forces between them. Here's what the equation says: An electric field is created by the presence of "electric charge". The field created this way points radially outward from the charge.
2. The second equation is mathematically the simplest, but is probably the most interesting. It doesn't have an official name, but is sometimes known as the "Gauss's Law of magnetism". Here's what it means: There is no such thing as "magnetic monopoles".
To understand what I mean by that phrase, recall something that you learned in grade school- that magnets have a 'north' end and a 'south' end. There is no such thing as a purely 'north' magnet or a 'south' magnet the way that positive and negative electric charges can be separated. That is precisely what the absence of magnetic monopoles suggests.
For comparison, while magnetism has dipoles (a loop of electric current; a single electron) but no monopoles, electricity has both monopoles (a single charge) and dipoles (a positive and negative charge right next to each other). Gravity, on the other hand, has monopoles but no dipoles (since there is no such thing as "negative mass"). To this day, there is ongoing research that is attempting to find evidence of magnetic monopoles. The presence of magnetic monopoles would not only make Maxwell's equations completely symmetric, but also clear up many mysteries in higher theories.
3. Equation 3 is interesting for another reason. It is known as Faraday's law, and gives half of the relationship between the electric and magnetic fields. Here's what it means: An electric field is created by a changing magnetic field. This equation is the principle behind how electric generators work, and makes the futuristic idea behind the 'rail gun' possible. To get the full picture of this equation's significance, you need to look at the last equation, too.
4. Equation 4 is called the Ampere-Maxwell equation. The reason it is named after two people is that the two terms were discovered separately. The first term states that a magnetic field is created around an electric current. In case you don't know, an electric current is merely the movement of electric charge. So let's review: An electric charge always creates an electric field, but when it moves, it also creates a magnetic field. This effect was first observed by Hans Oersted when he noticed that a compass needle was deflected by a current traveling through a wire. That simple observation, made while preparing for a lecture, would turn the physics world upside-down, as it was the first observation to link electric and magnetic effects- before that, they were thought to be separate phenomena.
The second term of the Ampere-Maxwell equation is technically the only thing that Maxwell actually discovered, which might make the term "Maxwell's equations" a bit of a misnomer. What the second term says is that a magnetic field is created by a changing electric field. Not only does this term show beautiful symmetry with Faraday's law, it would also be the key that would open the world to a whole mess of newly discovered physics.
The completion of Maxwell's equations had an affect on physics similar to what the development of quantum mechanics had much later. It not only changed how people viewed the effects of electricity and magnetism, but revolutionized (of all things) the field of optics.
What?!!!! Isn't optics the study of light???? What does that have to do with electricity and magnetism?
What Maxwell actually did was take equations 3 and 4, and putting them together, arrived at the wave equation- proving the existence of electromagnetic waves. Those two equations contain information on what these waves look like, as well as what their velocity is (hint: does 3x10^8 m/s sound familiar?). Further experiments later proved that these electromagnetic waves were, indeed, light- ushering in the wave model of optics.
So, everything you learned about optics in high school physics- from snell's law, lenses, diffraction, and more- can all be derived directly from Maxwell's equations (things that still could not be explained: atomic spectra, photoelectric effect, compton scattering).
To reiterate: Maxwell's equations were developed through experiments in 'electricity' and 'magnetism', involving things like glass rods, cat's fur, compass needles, batteries, and wire. Not only did these experiments establish that the two phenomena were intricately related, they also established the equations that would later be used to successfully predict a set of phenomena that no one ever thought was related.
I hope I just blew your mind.
But not only that: Maxwell's equations established that the speed of light was a constant. This fact, along with the experimental work of many others, was the starting point in Einstein's special relativity.
When special relativity is applied, Maxwell's equations also predict more phenomena, including bremsstrahlung, which predicts that accelerating charged particles emit radiation. This is the main source of heat in modern microwaves, and is being investigated as a method of active interrogation of supply trucks to combat nuclear threats.
There's more, but I think this post is getting a little long...
Monday, February 9, 2009
What I don't like about physics
One of the first things my wife ever asked me was the question, "Why do you like physics?" I don't think I ever answered that question for her- or at least not directly. After all, I don't think I really had a good answer back then.
The reason I chose to study physics was pretty simple: I felt that I was good at it. I chose to study physics while taking an advanced placement physics course in high school with my older brother. The classroom was filled with some of the smartest kids in school, many of whom were struggling pathetically- asking stupid questions with obviously no clue as to how to do any of the problems. I don't mean to brag, but I slept through class every other day and aced pretty much every test. Yes, I suppose I must be a genius, and that's just me being modest.
But, the question my wife asked was "Why do you like physics?", which requires a different answer entirely. I think I have a much better idea today than I did way back then, but it is still a question that I am hesitant to answer.
After all, when was the last time you heard someone say the phrase "I love physics" without having to wonder how long it has been since he last brushed his teeth?....or at least wonder how many hours he spends leveling up his elven rogue. I also feel that people who talk about physics a lot do so under the impression that people are impressed by it. Take the following conversation:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........You must be really smart!"
Yeah, so you may think that the person in the conversation above is impressed with my intellectual mastery, but if you could see the facial expressions that accompany the dialogue, you would probably have a different idea. Lets revisit the above conversation, but instead here's what the people involved are actually thinking:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........Why would you do that to yourself?"
"I suppose our conversation is over, huh?"
"Yeah.....So what level is your elven rogue?"
In college I learned to hate that conversation. Nevertheless, I'm still going to try to answer that question that my wife asked so long ago. Just keep in mind that physicists can still be cool. Richard Feynman is proof.
I've been typing for a while, and its late so maybe I'll do it later.
The reason I chose to study physics was pretty simple: I felt that I was good at it. I chose to study physics while taking an advanced placement physics course in high school with my older brother. The classroom was filled with some of the smartest kids in school, many of whom were struggling pathetically- asking stupid questions with obviously no clue as to how to do any of the problems. I don't mean to brag, but I slept through class every other day and aced pretty much every test. Yes, I suppose I must be a genius, and that's just me being modest.
But, the question my wife asked was "Why do you like physics?", which requires a different answer entirely. I think I have a much better idea today than I did way back then, but it is still a question that I am hesitant to answer.
After all, when was the last time you heard someone say the phrase "I love physics" without having to wonder how long it has been since he last brushed his teeth?....or at least wonder how many hours he spends leveling up his elven rogue. I also feel that people who talk about physics a lot do so under the impression that people are impressed by it. Take the following conversation:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........You must be really smart!"
Yeah, so you may think that the person in the conversation above is impressed with my intellectual mastery, but if you could see the facial expressions that accompany the dialogue, you would probably have a different idea. Lets revisit the above conversation, but instead here's what the people involved are actually thinking:
"So, what's your major?"
"Physics"
"Oh Really?!!!...........Why would you do that to yourself?"
"I suppose our conversation is over, huh?"
"Yeah.....So what level is your elven rogue?"
In college I learned to hate that conversation. Nevertheless, I'm still going to try to answer that question that my wife asked so long ago. Just keep in mind that physicists can still be cool. Richard Feynman is proof.
I've been typing for a while, and its late so maybe I'll do it later.
Tuesday, February 3, 2009
'Adulthood'
I've wondered for the past few years about how much the concept of 'adulthood' is just a front. As kids, we all looked at our parents, teachers, and others who were significantly larger than we were as if they were something great. Adulthood was an eternity away, and those who had reached it were full of experiences and knowledge beyond our comprehension. Adults could answer every question and solve every problem. They spent their time doing 'important' things that we were unfit to do. They hardly laughed, and when they did it was over things that we didn't understand. They never made mistakes.
As a kid I thought that children and adults lied in completely separate categories, as though there was a line drawn somewhere that was used to distinguish between the two. In my head, there was an age that someone reached, or a test that someone took, that once passed, would mark the exact time when a child had become an adult- complete with all the attributes and abilities that I thought all adults had.
But now is the time when I have to challenge this idea of 'Adulthood'. I am continuously faced with the question: "Am I an adult yet?" I do not think there is a real answer, but I still ask.
Of course, a government or religion can give a definition of what an adult is, but they are usually too simple to agree with the preconceptions that I've carried over from my grade school years.
Maybe I ask the question because I find myself in situations that bring it up. Like, for example, when I go searching for a job (a very adult-like activity), and the following conversation comes up:
"Excuse me, are you currently hiring teachers?"
"Maybe...........who's applying?"
"Me"
"You?.........Really?"
"Yes......I have a B.A. from UC Berkeley, and teaching experience."
"REALLY?..........But you look so young!!"
Things are generally much worse when the facts come out that: 1. I'm married, and 2. We're expecting a kid in a few months.
...which brings me to perhaps the real reason that I'm writing on this topic.
I play video games. I watch cartoons. I have a weekly ritual every Thursday night when I wait for the next Naruto issue to appear online and read it as fast as I can (sometimes getting enormously disappointed when it doesn't come). Although I still feel pretty 'adult' in some aspects, I'm sure that these are just some of the things that are ruining the image I described above. I don't feel that I will ever be an 'adult', so long as it is defined in the way that I thought it was when I was a kid.
Yet I still can't shake the idea that adults are supposed to be like in the picture I described. When I think of how I saw my parents and teachers as a child, I still feel that I will never reach the example that they have set for me. Am I just that childish?
Or, there is the other scenario, which is both liberating and somewhat disturbing: Maybe no one really grows up. Maybe they hold onto their childish tendencies, hiding them in front of onlookers in order to keep up the image. I wonder if the adults from my childhood still secretly laughed at fart jokes and did stupid things from time to time. I wonder if I'll have to maintain the front in front of my kids in a few years... or maybe I'll get to read Naruto with them.
As a kid I thought that children and adults lied in completely separate categories, as though there was a line drawn somewhere that was used to distinguish between the two. In my head, there was an age that someone reached, or a test that someone took, that once passed, would mark the exact time when a child had become an adult- complete with all the attributes and abilities that I thought all adults had.
But now is the time when I have to challenge this idea of 'Adulthood'. I am continuously faced with the question: "Am I an adult yet?" I do not think there is a real answer, but I still ask.
Of course, a government or religion can give a definition of what an adult is, but they are usually too simple to agree with the preconceptions that I've carried over from my grade school years.
Maybe I ask the question because I find myself in situations that bring it up. Like, for example, when I go searching for a job (a very adult-like activity), and the following conversation comes up:
"Excuse me, are you currently hiring teachers?"
"Maybe...........who's applying?"
"Me"
"You?.........Really?"
"Yes......I have a B.A. from UC Berkeley, and teaching experience."
"REALLY?..........But you look so young!!"
Things are generally much worse when the facts come out that: 1. I'm married, and 2. We're expecting a kid in a few months.
...which brings me to perhaps the real reason that I'm writing on this topic.
I play video games. I watch cartoons. I have a weekly ritual every Thursday night when I wait for the next Naruto issue to appear online and read it as fast as I can (sometimes getting enormously disappointed when it doesn't come). Although I still feel pretty 'adult' in some aspects, I'm sure that these are just some of the things that are ruining the image I described above. I don't feel that I will ever be an 'adult', so long as it is defined in the way that I thought it was when I was a kid.
Yet I still can't shake the idea that adults are supposed to be like in the picture I described. When I think of how I saw my parents and teachers as a child, I still feel that I will never reach the example that they have set for me. Am I just that childish?
Or, there is the other scenario, which is both liberating and somewhat disturbing: Maybe no one really grows up. Maybe they hold onto their childish tendencies, hiding them in front of onlookers in order to keep up the image. I wonder if the adults from my childhood still secretly laughed at fart jokes and did stupid things from time to time. I wonder if I'll have to maintain the front in front of my kids in a few years... or maybe I'll get to read Naruto with them.
Subscribe to:
Posts (Atom)
