The Heisenberg uncertainty principle is something much more specific, and much more interesting. It is a piece of the weirdness of quantum mechanics all wrapped up in simple mathematics. In case you are wondering why I never mentioned it in the definition of quantum mechanics that I wrote in the previous post, the answer is that I didn't have to. The Heisenberg uncertainty principle can be derived explicitly from what was written there. Thus, any evidence that violates this principle in turn violates all of quantum mechanics. Luckily (or unluckily), no one has ever found any such evidence (despite the efforts of many, with none other than Albert Einstein at the head).
So what does the Heisenberg uncertainty principle say?
Well, in quantum mechanics, there are many observable quantities, like position, momentum, angular momentum, energy, etc. The Heisenberg uncertainty principle states that certain pairs of observable quantities are incompatible, which means that it is impossible to know both quantities of a particular particle simultaneously to a certain level of certainty. There are many such incompatible pairs, the most famous of which is position and momentum. Other pairs include time and energy, and orthogonal components of angular momentum. The position-momentum uncertainty principle is mathematically represented like this:


Heisenberg showed evidence for this principle by asking what would happen if one were to try and measure either of these quantities. For example, imagine you have a particle inside a box, and you wish to measure its precise location.
So, to find the location of the particle, you might open a window and shine a light inside, and then study the light that is scattered off of the particle. In this way, you can know where the particle was at the instant you shined the light on it to arbitrary accuracy. However, the light you shine on the particle, by scattering off of it, can impart a wide range of possible momentum into it. As a matter of fact, if you would like to decrease the uncertainty behind your position measurement, you would have to use light of shorter wavelength, which has higher momentum and would produce a wider spread in the particle's resulting momentum distribution (by the way, to those of you who are familiar with the collapse of the wave function, this is one illustration of how it could actually happen- no sentient beings necessarily involved).
Measurements that would determine the momentum of a particle would similarly produce spreads in the position distribution in very real and concrete ways.
However, some would say that this argument is not entirely satisfactory, since it only shows how the position and momentum of a particle cannot both be known to arbitrary certainty. The Copenhagen interpretation insists that these values cannot even exist simultaneously. To even guess at the values would be in violation of the laws of physics.
In other words, a particle with perfectly defined position has momentum in all magnitudes simultaneously. A particle with perfectly defined momentum exists in all places in the universe.
However, another way to look at things might make this principle seem completely ordinary. In quantum theory, all particles are described by wave functions, not points. A particle's position is described by the position distribution of its wave function. The particle's momentum is described by the frequency distribution of the wave function.
Therefore, a particle with perfectly-defined position has a wave function that is a single spike- in mathematical terms, a Dirac delta function. A delta function has a frequency distribution that stretches to infinity in both directions, meaning that the momentum would have no definition at all.
On the other side, a particle with perfectly defined momentum would have a wave function that is an infinitely long sine wave. This function gives a spike in the frequency distribution, but extends to both sides of infinity in position-space.
This argument makes perfect mathematical sense (at least if you've taken a course in Fourier analysis). However, it is only valid if you assume that the wave function describes the entire state of the particle. Hidden variable theories claim that there is another piece to the puzzle- therefore, to prove the existence of a hidden variable, one would just have to show a situation with Heisenberg uncertainty violation. (Once again, Einstein himself tried and failed. Do you think you've got a shot?)
So, for those of you who are not yet entirely clear on this whole thing, lets look at what I think is the simplest example- spin states.
So, as you may know, certain particles like electrons and protons are called spin-1/2 particles. You may have heard that these particles have two spin states, commonly called spin-up and spin-down. Well, this picture omits a few details, so let's start over.
So, spin is a vector quantity that describes the innate angular momentum of certain particles. The fact that it is a vector quantity means that it has three components which we'll call the x-, y-, and z- components. What's special about spin is that for any particle, the magnitude of this vector is a constant, though each of the components is not.
Another interesting thing about spin is the fact that for spin-1/2 particles, there are exactly two stationary states corresponding to each spin component. So, for the z-component of spin, there are two stationary states, commonly called spin-up and spin-down. Likewise, looking at the x-component of spin, there are two different stationary states, which we'll agree to call spin-right and spin-left- for sake of the argument I'll present in a minute.
Now here's where things get interesting. It turns out that the three components of spin are incompatible in the Heisenberg sense. Therefore, if you know that an electron is in a spin-up state, the x- and y- components necessarily are undefined.
Imagine that you're on a plane, and you ask the flight attendant which direction you happen to be flying. She says, "We're headed in the eastern direction. As to whether we're headed north-east or south-east is undefined".
Bewildered, you ask the flight attendant if she could go to the cockpit and confer with the pilot whether they are headed north or south. The flight attendant returns, and says, "We're headed north, but now we don't know if we're headed north-east or north-west".
Now, let's imagine we're in a physics lab with an electron in a box. We measure the z-component of spin of this electron (let's not worry about how), and measure it to be in the spin-up state. Heisenberg comes by and says, "Now that the z-component is defined, the x-component is undefined and therefore has no value".
You say, "Poppycock! The x-component must be defined, or none of this makes sense! Why can't I just measure the x-component and find its value?"
So, you do the measurement along the x-axis, and now find that it is in the spin-right state.
You grin and exclaim, "Heisenberg, you're a fraud! This electron is spin-up and spin-right, thereby invalidating your uncertainty principle!"
Heisenberg responds, "Well, the particle was spin-up until you measured the spin along the x-axis. Now that the x-component is defined, the z-component is no longer. By making the second measurement, you caused the wave-function to collapse, thereby invalidating the first measurement."
You say, "Well, I never understood the wave-function collapse thing anyway. You'll have to provide another argument."
"Well, why don't you just measure the z-component once again?"
At this point two things could happen:
1: There is a 50% chance that you measure the particle to be spin-up again, in which case, you grin at Heisenberg until he convinces you to flip the coin again by measuring the x-component once more.
2: There is a 50% chance that the particle will now be spin-down. Now there's egg all over your face, since it is clear that the particle ceased to be spin-up as soon as you measured it to be spin-right. Otherwise, subsequent measurements of the z-component would always reveal it to be spin-up.
There's still one little caveat in this Heisenberg uncertainty business. That is, we still haven't really established what the cause of all this observation is. On the one hand, it could be an innate property of the particles involved. A particle known to be in a specific location just doesn't have a well-defined momentum. On the other hand, it could be a product of the effects of measurement. Strange mathematical coincidences regarding wave-function collapse make it impossible for the momentum to be known, but it may nevertheless exist. These two interpretations happen to be represented by two sides of the old quantum mechanics debate. On the one side is Niels Bohr with the Copenhagen interpretation- on the other, Albert Einstein and the hidden variables approach. Maybe I'll write more on that if this little girl in my lap will let me.
Maybe.

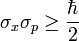
No comments:
Post a Comment